° Nombre tétraédrique. – Nombre figuré qui est engendré par un tétraèdre régulier. Les nombres tétraédriques de dimensions 2, 3, 4 et 5 sont définis.

n Nombre gnomonique tétraédrique ou tétraédrique D2
Nombre plan ou de dimension 2 qui est représenté par le gnomon d’un tétraèdre. Tout nombre de cette classe est la différence de deux tétraédriques D3 successifs. Le terme général est n(n + 1)/2. Les dix plus petits gnomoniques tétraédriques sont : 1, 3, 6, 10, 15, 21, 28, 36, 45 et 55. La suite des gnomoniques tétraédriques est la même que celle des triangulaires.

n Nombre tétraédrique ou tétraédrique D3
Nombre  polyédrique qui est engendré par un tétraèdre régulier. Tout nombre de rang n de cette classe est la somme des n premiers triangulaires. Le terme général est n(n + 1)(n + 2)/6. Les quatre plus petits tétraédriques D3 peuvent être représentés ainsi :

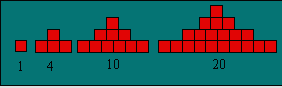
Un nombre est tétraédrique D3 si on peut décomposer son sextuple en trois facteurs qui sont trois entiers consécutifs. Son rang est le plus petit facteur. Pour trouver son successeur, on lui additionne le triangulaire de rang suivant. Par exemple, 969 est un tétraédrique car 969 × 6 = 17 × 18 × 19. Il est au rang 17. Son successeur est 969 + 171 = 1140. Les 39 plus petits tétraédriques D3 sont :

Voici quelques propriétés concernant les nombres de cette classe :

La période des unités des nombres successifs correspond à un nombre de 20 chiffres : 14 005 640 506 450 069 000.

Les unités sont 0, 1, 4, 5, 6 et 9.

La somme des n premiers tétraédriques D3 est un hypertétraédrique de rang n.

La différence de deux tétraédriques D3 successifs est un triangulaire.

Tout tétraédrique est la différence de deux  hypertétraédriques successifs.

La somme de deux tétraédriques D3 successifs est un pyramidal carré.

L’ensemble des tétraédriques D3 forme une suite arithmétique de degré 3.

 La suite des tétraédriques est la même que celle des pyramidaux triangulaires.

n Nombre hypertétraédrique ou tétraédrique D4
Nombre polyédrique de dimension 4 qui est engendré par un tétraèdre. Tout nombre de rang n de cette classe est la somme des n premiers tétraédriques D3. Le terme général est n(n + 1)(n + 2)(n + 3)/24. Les 29 plus petits hypertétraédriques sont :

Un nombre est hypertétraédrique si on peut décomposer 24 fois ce nombre en facteurs, soit quatre entiers consécutifs. Son rang est le plus petit facteur. Pour trouver son successeur, on lui additionne le tétraédrique de rang suivant. Par exemple, 1001 est un hypertétraédrique car 1001 × 24 = 11 × 12 × 13 × 14. Son rang est 11. Son successeur est 1001 + 364 = 1365. Voici quelques propriétés concernant les nombres de cette classe :

Les chiffres des unités sont 0, 1, 5 et 6.

La somme des n premiers hypertétraédriques est un tétraédrique D5 de rang n.

La différence de deux hypertétraédriques successifs est un tétraédrique D3.

Tout hypertétraédrique est la différence de deux tétraédriques D5 successifs.

L’ensemble des hypertétraédriques forme une suite arithmétique de degré 4.

La suite des hypertétraédriques est la même que celle des hyperpyramidaux triangulaires.

° Nombre tétraédrique D5
Nombre polyédrique de dimension 5 qui est engendré par un tétraèdre. Tout nombre de rang n de cette classe est la somme des n premiers hypertétraédriques. Le terme général est n(n + 1)(n + 2)(n + 3)(n + 4)/120. Les 10 plus petits tétraédriques D5 sont : 1, 6, 21, 56, 126, 252, 462, 792, 1287 et 2002. Les différences successives des suites à partir de la suite des tétraédriques D5 sont :

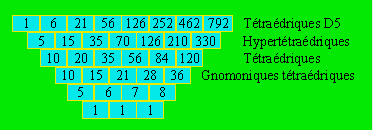
La suite des tétraédriques D5 est la même que celle des pyramidaux D5 triangulaires.

© Charles-É. Jean

Index : T