|
Carré
°
Nombre carré. –
Nombre
polygonal qui est engendré par un carré. Tout nombre de rang n
de cette classe est la somme des n premiers gnomoniques
carrés. Le terme général est n2.
Les cinq plus petits carrés peuvent être représentés ainsi :
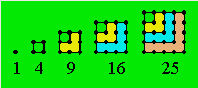
Un nombre est carré si, lui ayant soustrait 1, le résultat
est le produit de deux entiers dont la différence est 2. L’entier compris
entre les deux facteurs est le rang du carré. Pour trouver son successeur, on
lui additionne son rang et le rang suivant. Par exemple, 576 est un carré
car 575 = 23 × 25. Il est de rang 24. Son successeur est 576 + (24 + 25) = 625.
Voici un tableau qui contient les 99 plus petits carrés :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
1 |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
2 |
400 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
3 |
900 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
|
4 |
1600 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
|
5 |
2500 |
2601 |
2704 |
2809 |
2916 |
3025 |
3136 |
3249 |
3364 |
3481 |
|
6 |
3600 |
3721 |
3844 |
3969 |
4096 |
4225 |
4356 |
4489 |
4624 |
4761 |
|
7 |
4900 |
5041 |
5184 |
5329 |
5476 |
5625 |
5776 |
5929 |
6084 |
6241 |
|
8 |
6400 |
6561 |
6724 |
6889 |
7056 |
7225 |
7396 |
7569 |
7744 |
7921 |
|
9 |
8100 |
8281 |
8464 |
8649 |
8836 |
9025 |
9216 |
9409 |
9604 |
9801 |
Voici 14 propriétés concernant les nombres de cette classe :
La période des unités des nombres successifs correspond à un palindrome
de neuf chiffres, si on exclut le zéro : 149 656 941.
Les unités sont 0, 1, 4, 5, 6 et 9.
La somme des n premiers carrés est un pyramidal
carré de rang n.
La somme de deux carrés successifs est un centré
carré D2.
La différence de deux carrés successifs est un entier impair.
Tout carré est la différence de deux pyramidaux carrés successifs.
L'octuple d'un triangulaire
augmenté de 1 est un carré. (Diophante)
La somme de deux triangulaires successifs est un carré.
Tout carré de rang n est la somme de n et de deux fois le
triangulaire de rang (n - 1).
Tout entier est un carré ou est la somme de deux, trois ou quatre carrés.
(Fermat)
Tout entier naturel, sauf de la forme (4n + 2), peut être exprimé comme
la différence de deux carrés.
Tout carré auquel on soustrait 1 est un promèque
de classe d = 2.
Deux fois la somme de deux carrés de rangs n et (n + 1) moins 1
est un carré de rang (2n + 1).
L’ensemble des carrés forme une suite arithmétique
de degré 2.
Égalités
de carrés
On
peut trouver des égalités de carrés à partir de carrés magiques
d’ordres 3 et 4.
Carrés
magiques d’ordre 3
Dans
tout carré magique d’ordre 3, la somme des carrés des éléments de la
première ligne est égale à la somme des carrés des éléments de la
troisième ligne.
Preuve.
Soit un carré magique général d’ordre 3 dont la densité est 3a,
|
a + b
|
a – b – c
|
a + c
|
|
a – b + c
|
a
|
a + b – c
|
|
a – c
|
a + b + c
|
a – b
|
On
fait :
(a + b)2 + (a – b – c)2 + (a
+ c)2 = 3a2 + 2b2 + 2bc + 2c2
(a – c)2 + (a + b + c)2 + (a
– b)2 = 3a2 + 2b2 + 2bc + 2c2
Cas
particulier.
Posons a = 7, b = 3 et c = 2. On obtient ce carré magique.
On
peut écrire :
22
+ 92 + 102 = 42 + 52 + 122
= 185
Il
en est de même pour les colonnes de même rang.
L’égalité est :
52
+ 62 + 102 = 42 + 82 + 92
= 161
Carrés magiques d’ordre 4
Il
n’existe pas de règles générales qui permettent de trouver des égalités
de carrés dans les carrés magiques de cet ordre. On peut le faire à
partir de carrés généraux ou particuliers.
Carré
magique général
À
partir d’un carré magique général d’ordre 4, on peut trouver des égalités
de huit carrés dont
la somme de quatre carrés est égale à celle de quatre autres carrés.
Voici un tel carré :
|
3b + 3c
|
b
|
2b
|
3c
|
|
c
|
2b + 2c
|
b +
2c
|
3b + c
|
|
2c
|
2b + c
|
b + c
|
3b + 2c
|
|
3b
|
b +
3c
|
2b + 3c
|
0
|
Dans
ce carré magique, la densité est 6b + 6c. la somme des carrés des éléments
de la première ligne est égale à la somme des carrés des éléments de
la quatrième ligne. Leur somme est 14b2 + 18bc + 18c2.
Il
en est de même :
-
pour la deuxième et la troisième ligne. Leur somme est 14b2 +
18bc + 10c2.
-
pour la première et la quatrième colonne. Leur somme est 18b2
+ 18bc + 14c2.
-
pour la deuxième et troisième colonne Leur somme est 10b2 +
18bc + 14c2.
Si
b = 2 et c = 5, on obtient ce carré magique non normal dont la densité
est 42.
|
21
|
2
|
4
|
15
|
|
5
|
14
|
12
|
11
|
|
10
|
9
|
7
|
16
|
|
6
|
17
|
19
|
0
|
On
peut écrire :
22
+ 42 + 152 + 212 = 02 + 62
+ 172 + 192 = 686 (première et quatrième ligne)
52
+ 112 + 122 + 142 = 72 + 92
+ 102 + 162 = 486 (deuxième et troisième ligne)
52
+ 62 + 102 + 212 = 02 + 112
+ 152 + 162 = 602 (première et quatrième colonne)
22
+ 92 + 142 + 172 = 42 + 72
+ 122 + 192 = 570 (deuxième et troisième colonne)
De
plus, les deux diagonales ont des sommes qui permettent de trouver
d’autres égalités de carrés par rapport aux résultats précédents.
Diagonale
1 : 02 + 72 + 142 + 212 =
686
Diagonale
2 : 62 + 92 + 122 + 152 =
486
Carrés
magiques particuliers
Cas
1. Étudions
ce carré magique de numéro 21 dans l’index de Frénicle.
|
1
|
4
|
14
|
15
|
|
13
|
16
|
2
|
3
|
|
12
|
9
|
7
|
6
|
|
8
|
5
|
11
|
10
|
La
somme des carrés des éléments de la première ligne est égale à la
somme des carrés des éléments de la deuxième ligne.
12 + 42 + 142 + 152
= 22 + 32 + 132 + 162 = 438
La
somme des carrés des éléments de la troisième ligne est égale à la
somme des carrés des éléments de la quatrième ligne.
62 + 72 + 92 + 122
= 52 + 82 + 102 + 112 = 310
La
somme des carrés des éléments de la première colonne est égale à la
somme des carrés des éléments de la deuxième colonne.
12 + 82 + 122 + 132
= 42 + 52 + 92 + 162 = 378
La
somme des carrés des éléments de la troisième colonne est égale à la
somme des carrés des éléments de la quatrième colonne.
22 + 72 + 112 + 142
= 32 + 62 + 102 + 152 = 370
Cas
2. Étudions
ce carré magique de numéro 175 dans l’index de Frénicle.
|
16
|
2
|
3
|
13
|
|
5
|
11
|
10
|
8
|
|
9
|
7
|
6
|
12
|
|
4
|
14
|
15
|
1
|
La
somme des carrés des éléments de la première ligne est égale à la
somme des carrés des éléments de la quatrième ligne.
22 + 32 + 132 + 162
= 12 + 42 + 142 + 152 = 438
La
somme des carrés des éléments de la deuxième ligne est égale à la
somme des carrés des éléments de la troisième ligne.
52 + 82 + 102 + 112
= 62 + 72 + 92 + 122 = 310
La
somme des carrés des éléments de la première colonne est égale à la
somme des carrés des éléments de la quatrième colonne.
42 + 52 + 92 + 162
= 12 + 82 + 122 + 132 = 378
La
somme des carrés des éléments de la deuxième colonne est égale à la
somme des carrés des éléments de la troisième colonne.
22 + 72 + 112 + 142
= 32 + 62 + 102 + 152 = 370
De
plus, la somme des carrés des huit éléments des diagonales est égale
à la somme des carrés des huit éléments apparaissant en périphérie,
en excluant les coins. On a :
162
+ 112 + 62 + 12 + 132 + 102
+ 72 + 42 = 22 + 32 + 82
+ 122 + 152 + 142 + 92 + 52
= 748
Cas
3. Étudions un carré magique non normal dont la densité est
100.
|
49
|
6
|
2
|
43
|
|
8
|
37
|
41
|
14
|
|
36
|
9
|
13
|
42
|
|
7
|
48
|
44
|
1
|
Les
propriétés pour les lignes et les colonnes sont les mêmes que dans le
cas précédent. Aussi, on peut écrire :
22 + 62 + 432 + 492
= 12 + 72 + 442 + 482 = 4290
82 + 142 + 372 +
412 = 92 + 132 + 362 + 422
= 3310
72 + 82 + 362 + 492
= 12 + 142 + 422 + 432 = 3810
62 + 92 + 372 + 482
= 22 + 132 + 412 + 442 = 3790
De
plus, les diagonales brisées partagées en deux parties égales ont la même
propriété.
22
+ 142 + 362 + 482 = 62 + 82
+ 422 + 442 = 3800
Quand
on élève au cube chacun des éléments, on a aussi une égalité.
23
+ 143 + 363 + 483 = 63 + 83
+ 423 + 443 = 160 000.
Comme
dans le carré précédent, la somme des carrés des huit éléments des
deux diagonales est égale à la somme des carrés des huit éléments
apparaissant en périphérie, excluant les coins. On a :
492
+ 372 + 132 + 12 + 72 + 92
+ 412 + 432 = 62 + 22 + 142
+ 422 + 442 + 482 + 362 + 82
= 7600
Quand
on élève au cube chacun des éléments, on a aussi une égalité.
493
+ 373 + 133 + 13 + 73 + 93
+ 413 + 433 = 63 + 23 + 143
+ 423 + 443 + 483 + 363 + 83
= 320 000
Somme de deux carrés
Certains nombres s’expriment comme un
carré d’une seule façon. D’autres nombres peuvent s’exprimer comme
la somme de deux carrés de plus d’une façon.
Deux façons
Diophante a statué que le produit de
deux entiers dont chacun est la somme de deux carrés est aussi égale à
la somme de deux carrés. Cela se traduit ainsi :
(a² + b²)(c² + d²) = (ac + bd)² +
(ad - bc)²
(a²
+ b²)(c² + d²) = (ac - bd)² + (ad + bc)²
Pour trouver les
carrés, on établit la somme de deux paires de carrés. On multiplie les
deux sommes. Par exemple, on fait :
12 + 42 = 17
22 + 32 = 13
17 × 13 = 221
Le nombre 221 peut
s’exprimer d’au moins deux façons. On remplace les variables par leur
valeur. On obtient :
(a² + b²)(c² + d²) = (2 + 12)2
+ (3 – 8)2 = 142 + 52 = 221
(a² + b²)(c² + d²) = (2 – 12)2
+ (3 + 8)2 = 102 + 112 = 221
Les deux sommes sont : 142
+ 52 = 221 et 102 + 112 = 221.
Trois façons
Certains nombres peuvent s’exprimer
comme la somme de deux carrés d’au moins trois façons. Par exemple, on
écrit :
12 + 22 = 5
12 + 32 = 10
12 + 42 = 17
5 × 10 × 17 = 850
Le nombre 850 peut
s’exprimer d’au moins trois façons. On remplace les variables par
leur valeur en prenant deux égalités deux à deux. On obtient :
Avec 12 + 22 = 5 et
12 + 32 = 10, on trouve : 72 +
12 = 50 et 52 + 52 = 50.
Avec 72 + 12 = 50
et 12 + 42 = 17, on trouve : 112 +
272 = 850 et 292 + 32 =
850.
Avec 52 + 52 = 65
et 12 + 42 = 17, on trouve : 252 +
152 = 850 et 152 + 252 =
850.
Bref, 850 est la somme de deux carrés d’au moins
trois façons :
32 + 292 = 850
112 + 272 = 850
152 + 252 = 850
Douze carrés
On prend deux égalités de carrés ayant la même
valeur. On choisit un nombre, qu’on appelle opérateur, de préférence
supérieur à la plus grande base. De ce nombre, on soustrait chaque base
et on additionne la même base. On affecte chaque nombre de l’exposant
2. On obtient une égalité de carrés comportant le double de bases.
32 + 62 + 272 =
774
72 + 102 + 252 =
774
On choisit 28 comme opérateur. On fait : 28
– 3 = 25, 28 + 3 = 31, 28 – 6 = 22, 28 + 6 = 34, 28 – 27 = 1, 28 +
27 = 55. Ce sont les bases du premier membre de l’égalité. On fait :
28 – 7 = 21, 28 + 7 = 35, etc. Ce sont les bases du deuxième
membre de l’égalité. On peut écrire :
252 + 312 + 222 + 342 + 12
+ 552 = 212 + 352 + 182 + 382
+ 32 + 532 = 6252
Autres considérations
Les six plus petits nombres à la fois triangulaires et
carrés sont : 1, 36, 1225, 41 616, 1 413 721 et 48 024 900. Les triangulaires
sont successivement de rangs 1, 8, 49, 288, 1681 et 9800. Les carrés sont
successivement de rangs 1, 6, 35, 204, 1189 et 6930. Sachant que 1 et 6 sont les
deux plus petits rangs des carrés, on peut trouver chacun des successeurs en
multipliant le rang précédent par 6 et en soustrayant le rang antérieur. On a
ainsi : 6 × 6 - 1 = 35, 35 × 6 - 6 = 204, 204 × 6 - 35 = 1189, etc.
Le seul nombre supérieur à l'unité qui est à la fois
carré et pyramidal carré est 4900. Ce résultat fut conjecturé par Édouard
Lucas en 1875 et prouvé par G. N. Watson en 1918. Il existe seulement quatre
carrés de quatre chiffres dont tous les chiffres sont pairs : 4624, 6084, 6400
et 8464.
Certains chiffres peuvent être arrangés pour donner plus d’un
carré. Par exemple, avec 1, 6 et 9, on peut composer 169 = 132,
196 = 142,
961 = 312 ; avec 1, 2, 6
et 9, on peut composer 1296 = 362, 2916 = 542
et 9216 = 962. Certains carrés peuvent être
formés d'un autre carré auquel on ajoute des séquences de chiffres selon des
règles déterminées, comme dans ces deux exemples :
|
16 = 42 |
1156 = 342 |
111 556 = 3342 |
|
49 = 72 |
4489 = 672 |
444 889 = 6672 |
Les nombres carrés sont des nombres figurés.
Sous sa
forme arithmétique, un nombre carré est appelé carré
parfait.
© Charles-É. Jean
Index
: C
|
![]()
![]()