qui peut être représenté par un ensemble de
points disposés de façon régulière sur des hexagones. Les nombres centrés
hexagonaux de dimension inférieure ou égale à 5 sont définis ci-après.
n Nombre centré hexagonal
D1
Nombre centré linéaire
ou de dimension 1 dont les points sont disposés sur les côtés d’un
hexagone régulier. Tout nombre de rang n de cette classe, sauf 1, est un
multiple de 6. Les dix plus petits nombres de cette classe sont : 1, 6, 12,
18, 24, 30, 36, 42, 48, 54. Le terme général, en excluant 1, est 6(n -
1). Les quatre plus petits centrés hexagonaux D1 peuvent être représentés
ainsi :
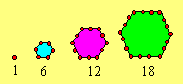
Pour trouver le rang d’un centré hexagonal D1, on divise
le nombre par 6 et on additionne 1 au quotient. Pour trouver son successeur, on
lui additionne 6. Par exemple, 42 est au rang 8 car 42 ÷ 6 = 7. Son successeur
est 48.
Voici cinq propriétés concernant cette classe de nombres :
Si on excepte le 1, la période des unités des
nombres successifs correspond à un nombre de cinq chiffres tous
différents et pairs : 62 840.
La somme des n plus petits centrés D1
hexagonaux est un centré
hexagonal D2 de rang n.
La somme de deux centrés D1 hexagonaux
successifs, en excluant 1, est égale à 12 fois le rang du plus petit moins 6.
Tout centré hexagonal D1 est la différence de
deux centrés hexagonaux D2 successifs.
Les nombres centrés D1 hexagonaux forment une
suite arithmétique de degré 1.
n Nombre centré
hexagonal D2
Nombre centré plan ou
de dimension 2 dont les points sont disposés sur les côtés parallèles d’hexagones
réguliers, ayant en plus un point au centre. Tout centré de rang n de
cette classe est la somme des n plus petits centrés
hexagonaux D1. Le terme général est (3n2
- 3n + 1). Les quatre plus petits centrés hexagonaux D2 peuvent être
représentés ainsi :
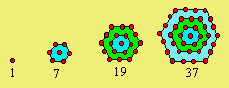
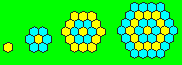
L’agencement d’hexagones réguliers permet d’illustrer
cette classe de nombres. En passant d’un rang à un autre, on ajoute une
couronne.
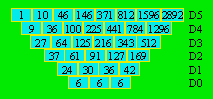
Les 39 plus petits centrés hexagonaux D2 sont :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
1 |
7 |
19 |
37 |
61 |
91 |
127 |
169 |
217 |
|
1 |
271 |
331 |
397 |
469 |
547 |
631 |
721 |
817 |
919 |
1027 |
|
2 |
1141 |
1261 |
1387 |
1519 |
1657 |
1801 |
1951 |
2107 |
2269 |
2437 |
|
3 |
2611 |
2791 |
2977 |
3169 |
3367 |
3571 |
3781 |
3997 |
4219 |
4447 |
Un nombre est de cette classe si, lui ayant soustrait 1 et
ayant divisé le résultat par 6, le quotient est un triangulaire.
Le rang du centré hexagonal D2 est supérieur de 1 à celui du triangulaire.
Pour trouver son successeur, on lui additionne six fois son rang. Par exemple,
217 est un centré hexagonal D2 car (217 - 1)/6 = 36 qui est le
triangulaire de rang 8. Aussi, 217 est au rang 9. Son successeur est 217 + (6 ×
9) = 271.
Voici six propriétés concernant cette classe de nombres :
La période des unités des nombres successifs
correspond à un palindrome
de cinq chiffres : 17 971.
Les unités sont 1, 7 et 9.
La somme des n plus petits centrés
hexagonaux D2 est un centré
hexagonal D3 de rang n.
La différence de deux centrés hexagonaux D2
successifs est le sextuple du rang le plus petit.
Tout centré hexagonal D2 est la différence de
deux cubes successifs.
Les nombres centrés hexagonaux D2 forment une
suite arithmétique de degré 2.
La suite des centrés hexagonaux D2 est la même que celle
des gnomoniques cubiques et celle des
centrés
étoilés triangulaires.
n Nombre centré
hexagonal D3
Nombre centré solide
ou de dimension 3 dont les points sont disposés sur un solide associé à
un hexagone régulier. Tout nombre de rang n de cette classe est la somme
des n plus petits centrés
hexagonaux D2. Le terme général est n(n2
+ 1)/2. La suite des centrés hexagonaux D3 est la même que celle des cubiques.
n Nombre centré
hexagonal D4
Nombre centré
hypersolide ou solide de
dimension 4 dont les points sont disposés sur un hypersolide associé à un
hexagone régulier. Tout nombre de rang n de cette classe est la somme
des n plus petits centrés
hexagonaux D3. Le terme général est n2(n
+ 1)2/4. La suite des centrés hexagonaux D4
est la même que celle des hypercubiques.
n Nombre centré
hexagonal D5
Nombre centré solide D5 ou
de dimension 5 dont les points sont disposés sur un solide de dimension 5
associé à un hexagone régulier. Tout nombre de rang n de cette classe
est la somme des n plus petits centrés
hexagonaux D4. Le terme général est n(n + 1)(n
+ 2)(3n2 + 6n + 1)/60. Les 10
plus petits centrés hexagonaux D5 sont : 1, 10, 46, 146, 371, 812, 1596,
2892, 4917, 7942 et 7942. Les différences successives des suites à partir de
la suite des centrés hexagonaux D5 sont :
La suite des centrés hexagonaux D5 est la même que celle
des cubiques D5.
![]()
![]()