Ceci est le septième article publié par Récréomath.

Carrés magiques d'ordre 3

Par Charles-É. Jean

Un carré est magique lorsque la somme des nombres de chaque ligne, de chaque colonne et de chaque diagonale est identique. Cette somme est appelée densité du carré magique. L’ordre du carré correspond au nombre d’éléments d’une ligne, d’une colonne ou d’une diagonale. Un carré d’ordre 3 contient huit rangées de trois éléments. Le médian est l’élément du centre.

Les éléments généralement utilisés pour former un carré magique d’ordre 3 sont les entiers consécutifs de 1 à 9. On parle alors de carré magique normal. Cependant, on peut utiliser certains autres ensembles de nombres. Voici l’unique carré magique normal d’ordre 3 dont la densité est 15 :

1. Propriétés des carrés magiques d’ordre 3
Pour former des carrés magiques d’ordre 3, il est parfois utile de connaître leurs propriétés. En voici sept :

La densité est égale au triple du médian. Si le médian est 7, la densité du carré est 21. Réciproquement, le médian est égal au tiers de la densité. Si la densité est 21, le médian est 7.

La densité est égale au tiers de la somme de ses éléments. Si la somme des éléments est 63, la densité est 21. Réciproquement, la somme des éléments est égale à trois fois la densité. Si la densité est 21, la somme des éléments est 63.

La somme des éléments est égale à neuf fois le médian. Si le médian est 7, la somme des éléments est 63. Réciproquement, le médian est égal au neuvième de la somme de ses éléments. Si la somme des éléments est 63, le médian est 63 ÷ 9 = 7.

La somme des éléments des quatre coins est égale à quatre fois le médian. Si le médian est 7, la somme des éléments des quatre coins est 28.

La somme des éléments des quatre coins est égale aux quatre tiers de la densité. Si la densité est 21, la somme des éléments des quatre coins est 28.

La somme des quatre éléments du centre de chaque rangée périphérique est égale à la somme des éléments des quatre coins.

La somme des deux éléments extrêmes d’une rangée qui passe par le centre est égale au double du médian. Si le médian est 7, la somme des deux éléments est 14.

Vérifiez ces propriétés dans le carré magique suivant.

2. Carrés magiques équivalents
Lorsqu’on déplace les éléments d’un carré magique d’ordre 3 par rotation autour d’un point ou par symétrie par rapport à un axe, on peut construire sept autres carrés magiques.

2.1 Par rotation
On considère le carré ci-dessus.

En faisant tourner le carré de 90° dans le sens horaire autour de la case centrale, on obtient le carré de gauche ci-dessous. En appliquant deux rotations successives de 90° sur chaque carré précédent, on obtient les deux autres carrés magiques.

Une autre rotation de 90° sur le dernier carré engendre le carré initial.

2.2 Par symétrie
Dans le carré magique de gauche, on considère la deuxième rangée horizontale comme l’axe de symétrie. En intervertissant les éléments symétriques de chaque colonne, on obtient le carré de droite.

Dans le carré magique de gauche, on considère la deuxième rangée verticale comme l’axe de symétrie. En intervertissant les éléments symétriques de chaque ligne, on obtient le carré de droite.

Dans le carré magique de gauche, on considère la diagonale qui contient 8 comme l’axe de symétrie. En intervertissant les éléments symétriques de chaque oblique, on obtient le carré de droite.

Dans le carré magique de gauche, on considère la diagonale qui contient 6 comme l’axe de symétrie. En intervertissant les éléments symétriques de chaque oblique, on obtient le carré de droite.

À partir d’un carré magique d’ordre 3, on peut donc obtenir trois autres carrés magiques par rotation et quatre autres carrés magiques par symétrie. Ces huit carrés magiques sont considérés comme équivalents.

3. Procédés de formation de carrés magiques
On peut former un carré magique d’ordre 3 notamment aux deux conditions suivantes :

Première condition. Les neuf nombres sont disposés en une suite arithmétique. Par exemple, on prend la suite 2, 5, 8, 11, 14, 17, 20, 23, 26 dont la raison est 3. On peut obtenir le carré magique ci-dessous dont la densité est 42.

Deuxième condition. Les neuf nombres sont disposés en trois suites arithmétiques de trois nombres ayant une même raison et les trois suites sont entre elles en progression arithmétique ayant une même raison. Par exemple, on prend les trois suites (2, 4, 6), (5, 7, 9), (8, 10, 12). La raison de chaque suite est 2. De plus, les éléments de même rang d’une suite à l’autre composent une suite arithmétique dont la raison est 3. On peut former le carré magique ci-dessous dont la densité est 21.

Nous vous présentons maintenant huit procédés permettant de construire des carrés magiques d’ordre 3.

3.1 À partir d’un nombre
Il est possible de construire une infinité de carrés magiques d’ordre 3 à partir d’un seul nombre. On prend, par exemple, 10. On le place au centre. Sur chacune des deux diagonales, on écrit deux nombres dont la somme est le double du nombre donné, soit 20. Voici la position des cinq premiers nombres :

On complète les cases vides de telle sorte que la densité soit 30. On obtient alors ce carré magique.

3.2 À partir de deux nombres
Il est possible de construire une infinité de carrés magiques d’ordre 3 à partir de deux nombres. On prend, par exemple, 10 et 16. On peut les placer de différentes façons. On explique ici deux situations.

1^e cas. On place les nombres aux extrémités d’une rangée qui passe par le centre. Comme la somme des deux nombres est 26, le médian est 13. On a alors :

La densité est 39. On complète la rangée horizontale supérieure, par exemple avec 8 et 21. On complète les diagonales, puis les deux colonnes. On obtient :

2^e cas. On place les nombres aux extrémités d’une rangée qui ne passe pas par le centre. On suppose un médian, par exemple 11. Si on ne veut pas avoir d’élément négatif, on choisit la valeur du médian entre les deux nombres donnés. On a :

On complète alors chacune des diagonales, puis les rangées périphériques. On peut obtenir ce carré magique.

On peut construire des carrés magiques d’ordre 3 à partir de trois nombres donnés. Toutefois, à partir de quatre nombres, il n’est pas possible de le faire dans tous les cas.

3.3 À partir d’un modèle connu
Les huit carrés magiques normaux sont les plus susceptibles de servir de modèles, car chaque élément de ce carré peut être associé à un rang. Ainsi, quand les éléments sont ordonnés, le premier élément est placé dans la case marquée 1, le deuxième dans la case 2, le troisième dans la case 3 et ainsi de suite. Voici un modèle :

Exemple 1. Soit l’ensemble dont les éléments sont en ordre magique : {3, 5, 7, 9, 11, 13, 15, 17, 19}, on place les éléments selon l’ordre du carré précédent. On obtient :

Exemple 2. Soit l’ensemble : {2, 5, 6, 8, 9, 10, 12, 13, 16}. Avant de placer les éléments dans un carré, il faut les mettre en ordre magique. Dans le premier ensemble, on place les deux plus petits éléments. La raison est 3. Le troisième élément sera 8. On a donc : {2, 5, 8}. Dans le deuxième ensemble, on place le plus petit élément qui reste, soit 6. On sait que la raison est 3. L’ensemble est alors : {6, 9, 12}. Le troisième ensemble est formé avec les nombres qui restent . On a {10, 13, 16}. L’ordre magique est : 2, 5, 8, 6, 9, 12, 10, 13, 16. On distribue les nombres dans le carré comme dans l’exemple précédent. On obtient :

3.4 À partir de combinaisons
On fait la liste des combinaisons de trois nombres dont la somme est égale à la densité. Par exemple, on veut construire un carré magique avec les entiers consécutifs de 3 à 11. La densité est alors 21. Les combinaisons possibles de trois nombres dont la somme est 21 sont : (3, 7, 11), (3, 8, 10), (4, 6, 11), (4, 7, 10), (4, 8, 9), (5, 6, 10), (5, 7, 9) et (6, 7, 8). Il existe donc huit combinaisons, sans tenir compte des permutations.

On établit un tableau de fréquence des éléments c’est-à-dire en comptant le nombre de fois que chaque nombre apparaît dans les huit combinaisons.

On attribue à chaque case du carré d’ordre 3 une cote d’utilité relative. En effet, chaque élément d’une case d’un angle est l’intersection de trois rangées, chaque élément central des cases périphériques est l’intersection de deux rangées et le médian l’intersection de quatre rangées. Voici la cote d’utilité relative pour chaque case :

On compare maintenant le tableau de fréquence avec le tableau des cotes d’utilité relative. Comme seul le 7 apparaît quatre fois dans les combinaisons, il est nécessairement le médian. Les éléments 4, 6, 8 et 10 apparaissent chacun trois fois. Ils sont donc dans les coins. On les place de façon à respecter la densité, puis on complète par calculs. Une disposition des nombres est :

3.5 Par un déplacement oblique
Lorsqu’on est certain que neuf nombres peuvent former un carré magique, on peut utiliser un procédé où on se déplace obliquement de gauche à droite et on revient dans le carré quand on doit en sortir.

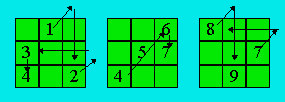
· Le premier élément est placé au centre de la première ligne.

· Le deuxième élément devrait apparaître dans la case supérieure de la troisième colonne. On le glisse dans la même colonne sur la troisième ligne.

· Le troisième élément devrait apparaître dans la case à droite de la deuxième ligne. On le glisse sur la même ligne dans la première colonne.

· Le quatrième élément est placé sous le troisième.

· Le cinquième et le sixième sont placés successivement sur la diagonale libre.

· Le septième est placé sous le sixième.

· Le huitième devrait apparaître dans la case à droite de la première ligne. On le glisse sur la même ligne dans la première colonne.

· Le neuvième élément devrait apparaître dans la case supérieure de la deuxième colonne. On le glisse dans la même colonne sur la troisième ligne.

Soit à former un carré magique dont les éléments sont : 4, 6, 7, 8, 9, 10, 11, 12, 14. On met d’abord les éléments en ordre comme il a été expliqué précédemment. On obtient : 4, 6, 8, 7, 9, 11, 10, 12, 14. On distribue les éléments ainsi :

3.6 D'après le rang des éléments
Les neuf éléments sont connus et sont en ordre magique. Voici un exemple : 2, 6, 10, 5, 9, 13, 8, 12, 16. L’élément du centre, soit le cinquième élément, devient le médian du carré magique. Les éléments de rang pair sont placés dans les coins. On les place de telle façon que les quatrième et sixième éléments soient sur la même diagonale : ce qui revient à dire qu’en suivant l’ordre, on place ces éléments en forme de Z droit ou inversé. Par la suite, on complète chaque rangée périphérique. On obtient ce carré magique :

3.7 En opérant sur des carrés magiques connus
On peut produire de nombreux carrés magiques en additionnant n’importe lequel nombre aux éléments d’un carré magique connu. Voici un exemple :

La densité du premier carré est 21 ; celle du second est 48. Il y a une différence de 3 × 9 = 27 entre les densités des deux carrés.

Au lieu de l’addition, on peut utiliser la soustraction, la multiplication ou la division. Voici un exemple de division :

La densité du premier carré est 45 ; celle du second est 15.

De plus, on peut additionner ou soustraire deux carrés magiques. Cela donne un troisième carré magique. Par exemple,

La densité du premier carré est 51 ; celle du deuxième est 15 ; celle du troisième est 51 + 15 = 66. Si on soustrait ces deux carrés au lieu de les additionner, on trouve ce nouveau carré magique dont la densité est 36 :

3.8 À partir d’un carré magique général
Deux situations différentes sont explicitées.

1^e cas. On compose le carré magique général directement dans la figure. Voici les étapes :

On pose d’abord a comme médian.

On complète une diagonale avec (a + b) et (a - b). La densité est alors 3a.

On complète l’autre diagonale avec (a + c) et (a - c).

Enfin, on complète chaque rangée pour avoir 3a comme densité.

En donnant à a, à b et à c des valeurs arbitraires, on aura chaque fois un nouveau carré magique. Par exemple, si a = 10, b = 3 et c = 4, on obtient :

2^e cas. On compose trois sous-ensembles et on place les éléments en se basant sur un modèle connu.

On pose a le plus petit élément et r la raison de la première suite de trois nombres. Cela donne : {a, a + r, a + 2r}.

On pose s la raison entre les suites. Le deuxième sous-ensemble est {a + s, a + r + s, a + 2r + s}. Le troisième est : {a + 2s, a + r + 2s, a + 2r + 2s}. En prenant le modèle de gauche, on aura :

La densité est 3a + 3r + 3s. En donnant à a, à r et à s des valeurs arbitraires, on aura chaque fois un nouveau carré magique. Par exemple, si a = 3, r = 1 et s = 4, on obtient :

Problèmes et recherche
Vous voulez relever des défis. Amusez-vous à résoudre les problèmes. Les solutions sont données à la fin.

Problème 1. Formez un carré magique d’ordre 3 avec l’ensemble suivant : {6, 11, 14, 16, 19, 22, 24, 27, 32}

Problème 2. Formez deux carrés magiques d'ordre 3 en utilisant les nombres 13, 15, 17, 21, 23, 25. Dans chaque cas, indiquez la densité.

Problème 3. Placez des nombres dans les cases vides pour que chacun des carrés soit magique et que tous les éléments soient différents.

Problème 4. Formez un carré magique d'ordre 3 avec ces quatre nombres : 5, 9, 11, 21.

Problème 5. Formez un carré magique d'ordre 3 dont la somme des quatre coins est 28 et dont le plus grand élément est 12.

Problème 6. En faisant une rotation de 270° dans le sens horaire, construisez un autre carré magique à partir du carré donné.

Problème 7. Formez un autre carré magique en déplaçant les éléments par symétrie si l’axe est  la diagonale qui contient 18.

Problème 8. À partir du carré magique ci-dessous, trouvez un autre carré magique en faisant successivement les opérations données : multipliez par 12, additionnez 39, divisez par 3 et soustrayez 21.

Problème 9. Un des éléments d’un carré magique est 12. Formez un carré magique d'ordre 3 dans chacun des cas.
a) La densité est 27.
b) Le plus petit élément est 5 et le plus grand est 31.

Problème 10. Formez un carré magique général d’ordre 3 dont les éléments forment une suite arithmétique de degré r.

 * * * * * * * *

Solution 1. Voici un des huit carrés magiques équivalents :

Solution 2. La densité du premier carré est 45 ; celle du second est 69.

Solution 3. Voici un carré magique dans chaque cas :

Solution 4. Voici un carré magique :

Solution 5. Voici un carré magique :

Solution 6. Le carré magique est :

Solution 7. Le carré magique est :

Solution 8. Soit a tout élément du carré magique donné. On fait les opérations suivantes : (12a + 39)/3 - 21 = 4a - 8 = 4(a - 2). Il s’agit alors de soustraire chaque élément de 2 et de multiplier par 4. On obtient :

Solution 9. Voici un carré magique dans chaque cas :

Solution 10. On pose a le plus petit élément. Le suivant est a + r. Les autres dans l’ordre magique sont : a + 2r, a + 3r, a + 4r, a + 5r, a + 6r, a + 7r et a + 8r. Voici un carré magique général :