Série A

Solution 20

Dans le coin supérieur gauche, on pourrait placer 7, 14 ou 21. Seul 14 est pair. On le place dans cette case. Dans le coin inférieur droit, on pourrait placer 4, 11 ou 18. Seul 4 convient. À cause de la somme 27, au centre on a 9. On place 12 dans le coin supérieur droit car c’est le seul pair possible. On complète en appliquant la somme. On obtient ce tableau.

Retour au problème

Cela a pris quatre ans avant qu’internet atteigne la masse critique de 20 % d’utilisateurs.

Série B

Solution 20

La somme des numéros de 1 à 12 est 78. En divisant 78 par 21, on obtient 3,71. Théoriquement, Zoélie peut former trois groupes. Or 3 × 21 = 63. On fait 78 - 63 = 15. On tente l’hypothèse où on exclut les gilets 3 et 12. On vérifie s’il est possible de regrouper les 10 enfants qui restent. On peut obtenir les groupes : (1, 2, 7, 11), (5, 6, 10), (4, 8, 9). 

Au maximum, 10 enfants peuvent appartenir aux groupes.

Retour au problème

Série C

Solution 20

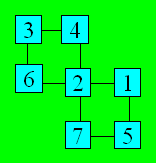
La somme des nombres de 1 à 7 est 28. Pour obtenir le double de 15, on additionne 2 à 28. On place 2 dans la cellule qui est le point de rencontre des deux carrés. Une configuration est :

Retour au problème