|
| |
|

|
Publications |
|
Ceci est le sixième livre édité par Récréomath.
Secrets des carrés
magiques d'ordre 3
Par Charles-É. Jean
|
* * *
Chapitre 5
Des trios de triplets
|
Sommaire. Arrangement des éléments.
Conditions pour former un trio magique. Construction d’un trio magique.
Construction d’un carré magique. Position des éléments dans un carré
magique. Forme générale d’un trio. Relations entre les raisons du trio et d’un
triplet. Trios équivalents. Carré image.
|
* * * * * * * * * * *
|
5.01 Arrangement des éléments
Sachant que neuf nombres sont les éléments d’un carré magique d’ordre
3, on peut disposer ces nombres en trois groupes de trois éléments appelés
triplets. L’ensemble de ces groupes est appelé trio. Soit l’ensemble
associé {a1, a2, a3, a4,
a5, a6, a7, a8,
a9}, alors (a1, a2, a3),
(a4 a5, a6) et (a7,
a8, a9) sont trois triplets magiques et {(a1,
a2, a3), (a4 a5,
a6), (a7, a8, a9)}
est un trio magique.
La différence entre les nombres voisins de chaque triplet
est appelée la raison du triplet. Elle doit être toujours la même et est
notée r. Ainsi, r = a2 - a1 =
a3 - a2 = a5
- a4 = a6 -
a5 = a8 - a7
= a9 - a8.
La différence entre chaque élément de même rang des
triplets voisins est appelée la raison du trio. Elle doit toujours être la
même et est notée r0. Ainsi, r0 = a4
- a1 = a5 -
a2 = a6 - a3
= a7 - a4 = a8
- a5 = a9 -
a6.
Par exemple, dans le trio {(15, 13, 11), (7, 5, 3), (-
1, - 3, - 5)}, r = -
2 et r0 = - 8.
5.02 Conditions pour former un trio magique
Pour avoir un trio magique, il faut que chaque triplet soit formé de trois
nombres qui sont en progression arithmétique et que les éléments de même
rang de chaque triplet soient aussi en progression arithmétique.
Soit le trio {(a1, a2,
a3), (a4, a5, a6),
(a7, a8, a9)}, si a1
= a2 et si a1 = a4, on
aura le trio : {(a1, a1,
a1), (a1, a1, a1),
{(a1, a1, a1)}. Alors, l’ensemble
associé est {a1} où r = r0 = 0.
Si a1 = a2, on aura le
trio : {(a1, a1, a1),
(a4, a4, a4), {(a7,
a7, a7)}. L’ensemble associé est {a1,
a4, a7}où r = 0 et r0
= a4 - a1.
Si a2 = a4, on aura le
trio : {(a1, a2, a3),
(a2, a3, a4), (a3,
a4, a5)}. L’ensemble associé est {a1,
a2, a3, a4, a5}où
r = r0 = a2 - a1.
Si a3 = a4, on aura le
trio : {(a1, a2, a3),
(a3, a4, a5), (a5,
a6, a7)}. L’ensemble associé est {a1,
a2, a3, a4, a5,
a6, a7}où r = a2 -
a1 et r0 = a3 - a1.
Si tous les éléments sont différents, on aura le
trio : {(a1, a2, a3),
(a4, a5, a6), (a7,
a8, a9)} où r = a2
- a1 et r0 = a4 - a1.
Il n’existe donc pas d’ensemble associé qui soit formé
d’un nombre pair d’éléments. En conséquence, on ne peut pas construire un
trio magique avec deux, quatre, six ou huit nombres différents.
5.03 Construction d’un trio magique
Connaissant neuf nombres qui forment un carré magique, on peut construire
un trio d’abord en plaçant ces nombres en ordre croissant ou décroissant.
n L’ensemble associé est
formé par neuf éléments différents. Trois cas peuvent se présenter :
• Si tous les éléments sont en progression arithmétique,
alors on conserve cet ordre pour construire le trio. Soit l’ensemble associé
{2, 4, 6, 8, 10, 12, 14, 16, 18}, le trio est : {(2, 4, 6), (8, 10, 12),
(14, 16,18)}.
• Si les éléments sont en progression arithmétique trois
par trois, alors on conserve cet ordre pour construire le trio. Soit l’ensemble
associé {1, 3, 5, 8, 10, 12, 15, 17, 19}, le trio est : {(1, 3, 5), (8,
10, 12), (15, 17, 19)}
• Si les éléments, une fois en ordre numérique, ne sont
pas en progression arithmétique, on place d’abord trois nombres dans les
mêmes positions : le plus petit, celui du milieu et le plus grand. On
place le deuxième plus petit nombre en deuxième position. Cela permet de
connaître la raison des triplets. On complète chacun des triplets. Soit l’ensemble
associé {3, 6, 7, 9, 10, 11, 13, 14, 17}, le trio est : {(3, 6, 9), (7,
10, 13), (11, 14, 17)}.
n L’ensemble associé est
formé par sept éléments en progression arithmétique. On écrit deux fois le
troisième et le cinquième élément de l’ensemble associé. Soit l’ensemble
associé {5, 10, 15, 20, 15, 30, 35}, le trio est : {(5, 10, 15), (15, 20,
25), (25, 30, 35)}. On peut vérifier que 2r = r0.
n L’ensemble associé est
formé par cinq éléments en progression arithmétique. On écrit deux fois le
deuxième élément, trois fois le troisième et deux fois le quatrième. Comme
les nombres ne sont pas en progression arithmétique, on intervertit le
troisième et le quatrième élément, puis le sixième et le septième
élément. Soit l’ensemble associé {3, 5, 7, 9, 11}, le trio est : {(3,
5, 7), (5, 7, 9), (7, 9, 11)}. On peut vérifier que r = r0.
n L’ensemble associé est
formé par trois éléments en progression arithmétique. On écrit trois fois
chaque élément. Soit l’ensemble associé {5, 8, 11}, le trio est : {(5,
5, 5), (8, 8, 8), (11, 11, 11)}. On peut vérifier que r = 0 et r0
¹ 0.
n L’ensemble associé est
formé par un élément. On écrit neuf fois le même élément. Soit l’ensemble
associé {5}, le trio est : {(5, 5, 5,), (5, 5, 5), (5, 5, 5)}. On peut
vérifier que r = r0 = 0.
5.04 Construction d’un carré magique
À partir d’un trio formé précédemment, il est possible de construire
un carré magique d’ordre 3 en procédant ainsi :
1. On place le premier élément du premier triplet au centre
de la première ligne.
2. Chaque élément suivant est placé dans la colonne
voisine sur la ligne supérieure.
3. Si le lieu approprié est en dehors du carré :
a) tout élément de la ligne supérieure à la première
ligne est placé sur la ligne 3 dans la même colonne.
b) tout élément de la colonne voisine de la troisième
colonne est placé dans la colonne 1 sur la même ligne.
4. Si le lieu approprié et déjà occupé, on place l’élément
sous le dernier inscrit.
Soit le trio {(a1, a2,
a3), (a4, a5, a6),
(a7, a8, a9)}, on procède
ainsi.
|
· |
a 1 |
· |
|
· |
a 1 |
· |
|
· |
a 1 |
· |
|
· |
· |
· |
|
· |
· |
· |
|
a 3 |
· |
· |
|
· |
· |
· |
|
· |
· |
a 2 |
|
· |
· |
a 2 |
|
· |
a 1 |
· |
|
· |
a 1 |
· |
|
· |
a 1 |
a 6 |
|
a 3 |
· |
· |
|
a 3 |
a5 |
· |
|
a 3 |
a5 |
· |
|
a 4 |
· |
a 2 |
|
a 4 |
· |
a 2 |
|
a 4 |
· |
a 2 |
|
· |
a 1 |
a 6 |
|
a 8 |
a 1 |
a 6 |
|
a 8 |
a 1 |
a 6 |
|
a 3 |
a5 |
a 7 |
|
a 3 |
a5 |
a 7 |
|
a 3 |
a5 |
a 7 |
|
a 4 |
· |
a 2 |
|
a 4 |
· |
a 2 |
|
a 4 |
a 9 |
a 2 |
|
|
Par exemple, le carré magique correspondant au trio :
{(3, 6, 9), (4, 7, 10), (5, 8, 11)} est :
Lorsque les éléments sont placés en ordre numérique
croissant dans tout triplet, la raison du triplet est positive ; le carré
magique engendré est dit ascendant par rapport aux triplets. Lorsque les
éléments sont placés en ordre numérique décroissant dans tout triplet, la
raison du triplet est négative ; le carré magique est dit descendant.
Lorsque les éléments sont placés en ordre numérique
croissant d’un triplet à l’autre, la raison du trio est positive et le
carré magique engendré est dit ascendant par rapport au trio. Lorsque les
éléments sont placés en ordre numérique décroissant d’un triplet à l’autre,
la raison du trio est négative et le carré magique est dit descendant par
rapport au trio.
|
|
Par exemple, le carré ci-contre est un carré magique
ascendant par rapport aux triplets car r = 2 et descendant par rapport au
trio car r 0
= -3.
À partir d’un carré magique, on peut écrire le trio en
repérant les éléments du carré dans l’ordre où on les a écrits selon la
technique de formation décrite. Soit le carré magique :
le trio correspondant est : {(1, 3, 5), (7, 9, 11), (13,
15, 17)}.
|
|
5.05 Position des éléments dans un carré magique
Tout élément qui appartient à un carré magique ne peut pas occuper n’importe
laquelle position. Pour le vérifier, prenons neuf nombres différents qui
forment un carré magique : {1, 4, 6, 7, 9, 11, 12, 14, 17}. Comme la somme
des éléments est 81, la densité du carré magique sera 27. Il existe huit
combinaisons de trois nombres dont la somme est 27. Les voici :
1 + 9 + 17 = 27
1 + 12 + 14 = 27
4 + 6 + 17 = 27 4 +
9 + 14 = 27
1 + 12 + 14 = 27
4 + 6 + 17 = 27
4 +
9 + 14 = 27
4 + 11 + 12 = 27
6 + 7 + 14 = 27
6 + 9 + 12 = 27
7 + 9 + 11 = 27
Le tableau suivant indique le nombre de fois (fréquence) où
chaque élément apparaît dans les combinaisons.
|
Élément |
1 |
4 |
7 |
6 |
9 |
12 |
11 |
14 |
17 |
|
Fréquence |
2 |
3 |
2 |
3 |
4 |
3 |
2 |
3 |
2 |
Les éléments doivent être placés dans le carré magique
selon les règles suivantes :
• Tout nombre dont la fréquence est 2 est un élément
central des rangées périphériques : il est à l’intersection d’une
ligne et d’une colonne. Les éléments sont a12, a21,
a23 et a32 (diagramme A).
• Tout nombre dont la fréquence est 3 est un élément des
angles : il est à l’intersection d’une ligne, d’une colonne et d’une
diagonale. Les éléments sont a11, a13, a31
et a33 (diagramme B).
• Le nombre dont la fréquence est 4 est le médian :
il est à l’intersection de la deuxième ligne et de la deuxième colonne,
également des deux diagonales. L’élément est a22
(diagramme C).
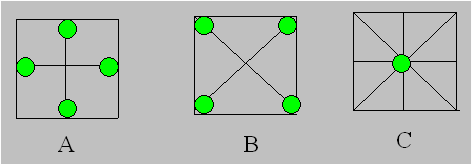
Par rapport à l’ensemble {1, 4, 6, 7,
9, 11, 12, 14, 17}, les éléments 1, 7, 11, 17 correspondent à a12,
a21, a23 ou a32 ; 4,
6, 12, 14 correspondent à a11, a13, a31
ou a33 ; 9 correspond à a22.
Soit {(a1, a2,
a3), (a4, a5, a6),
(a7, a8, a9), on
peut généraliser le tableau des fréquences :
|
Élément |
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
a 6 |
a 7 |
a 8 |
a 9 |
|
Fréquence |
2 |
3 |
2 |
3 |
4 |
3 |
2 |
3 |
2 |
Si l’ensemble associé contient moins de neuf éléments,
on complète le trio et on procède ensuite de la même façon que
précédemment.
Soit l’ensemble associé {6, 7, 8, 9, 10}, on a le trio
{(6, 7, 8), (7, 8, 9), (8, 9, 10)}. Le tableau des fréquences est :
|
Élément |
6 |
7 |
8 |
7 |
8 |
9 |
8 |
9 |
10 |
|
Fréquence |
2 |
3 |
2 |
3 |
4 |
3 |
2 |
3 |
2 |
• 6, 10 correspondent à a12 ou a32,
a21 ou a23 : chaque élément apparaît une
fois dans le carré magique.
• 7, 9 correspondent à a11, a13,
a31 ou a33 : chaque élément apparaît
deux fois dans le carré magique.
• 8 correspond à a12 ou a32,
a21 ou a23 et à a22
: cet élément apparaît trois fois dans le carré magique.
|
|
5.06 Forme générale d’un trio
Soit a le premier élément d’un ensemble de neuf nombres qui
forment un carré magique, r et r0 les raisons
respectives du triplet et du trio, alors la forme générale du trio est : {(a,
a + r, a + 2r), (a + r0, a
+ r + r0, a + 2r + r0), (a
+ 2r0, a + r + 2r0, a +
2r +2r0)}
Le carré magique découlant de ce trio est :
|
a +
r + 2r0 |
a |
a +
2r + r0 |
|
a +
2r |
a + r
+ r0 |
a +
2r0 |
|
a + r0 |
a +
2r + 2r0 |
a + r |
La densité de ce carré magique est : 3(a + r
+ r0) ou 3a + 3r + 3r0.
Problème 1. Sachant que le plus petit élément d’un
carré magique est 3, que les raisons du triplet et du trio sont respectivement
5 et - 1, construisez le carré magique.
|
|
Solution. Le trio est {(3, 8, 13), (2, 7, 12), (1, 6, 11)}.
Le carré magique correspondant est :
Problème 2. La densité d d’un carré magique est
63. Les raisons du triplet et du trio sont respectivement 2 et 3. Construisez le
carré magique.
Solution. Le médian m est 21 car m
= d/3. Le premier élément est égal à m
- r - r0,
soit 21 - 2 -
3 = 16. Le trio est : {(16, 18, 20), (19, 21, 23), (22, 24, 26)}. Le carré
magique correspondant est :
|
24 |
16 |
23 |
|
20 |
21 |
22 |
|
19 |
26 |
18 |
|
|
Problème 3. La densité d’un carré magique est 99. Le
plus petit nombre est 20 et la raison du trio est 10. Construisez le carré
magique.
Solution. Le premier élément du deuxième triplet
est 30 car le plus petit nombre est 20 et la raison du trio est 10.
Le médian m est 33 car m = d/3. On fait : 33 -
30 = 3. D’où r = 3. Le trio est {(20, 23, 26), (30, 33, 36),
(40, 43, 46)}. Le carré magique correspondant est :
|
43 |
20 |
36 |
|
26 |
33 |
40 |
|
30 |
46 |
23 |
|
|
5.07 Relations entre les raison du trio et d’un triplet
Lorsque neuf nombres sont en progression arithmétique, ils forment un trio
et la raison du trio est le triple de la raison d’un triplet.
Soit p la raison d’une progression arithmétique et a
le plus petit nombre, l’ensemble associé est : {a,
a + p, a + 2p, a + 3p, a + 4p,
a + 5p, a + 6p, a + 7p, a + 8p}.
Le trio est: {(a, a + p, a + 2p), (a +
3p, a + 4p, a + 5p), (a + 6p, a
+ 7p, a + 8p)}.
r = p et r0 = 3p.
D’où
r0 = 3r. Le carré magique
correspondant est :
|
a +
7p |
a |
a +
5p |
|
a +
2p |
a +
4p |
a +
6p |
|
a +
3p |
a +
8p |
a + p |
La densité d du carré magique est 3(a + 4p)
ou 3a + 12p. La somme S des éléments est 9(a + 4p)
ou 9a + 36p.
Soit 1 le plus petit nombre d’une progression arithmétique
de raison 1. Le trio est : {(1, 2, 3), (4, 5, 6), (7, 8, 9)}. On a : r
= 1 et r0 = 3. Le carré magique
correspondant est :
d = 15 et S = 45. On peut vérifier que m = a +
r + r0 = 1 + 1 + 3 = 5.
|
|
Sachant que les éléments d’un carré magique sont en
progression arithmétique de raison p et connaissant la densité du
carré magique, on peut trouver le plus petit nombre.
Puisque m = a + r + r0,
alors a = m -
r - r0.
D’où, a = m - 4p.
Problème 1. La densité d’un carré magique est 57 et la
raison de la progression arithmétique est 5. Construisez le carré magique.
Solution. d = 57 d’où m = 19. Alors, a
= m - 4p = 19 – 20 = -
1. Le trio est {(- 1, 4, 9), (14, 19, 24),
(29, 34, 39)}. Le carré magique correspondant est :
|
34 |
- 1 |
24 |
|
9 |
19 |
29 |
|
14 |
39 |
4 |
Si la raison de la progression arithmétique était -
5 au lieu de 5, on aurait : a
= m - 4p = 19
+ 20 = 39. Le trio est : {(39, 34, 29), (24, 19, 14), (9, 4, -1)}. Le
carré magique correspondant est :
|
4 |
39 |
14 |
|
29 |
19 |
9 |
|
24 |
- 1 |
34 |
On obtient donc un carré magique équivalent.
|
|
Problème 2. La densité d’un carré magique est 102 et le
plus petit élément de la progression arithmétique est 8. Calculez la raison
de la progression et construisez le carré magique.
Solution. La densité est 102. D’où le médian est 34.
Comme a = m - 4p,
alors p = (m - a)/4
= (34 - 8)/4 = 6½.
Le trio est : {(8, 14½, 21), (27½,
34, 40½), (47, 53½, 60)}. Le
carré magique correspondant est :
|
53 ½ |
8 |
40 ½ |
|
21 |
34 |
47 |
|
27 ½ |
60 |
14 ½ |
|
|
Problème 3. Le plus petit élément d’une progression
arithmétique de raison 8 est 12. Calculer la densité sans construire le carré
magique.
Solution. Puisque a = m -
4p,
alors m = a + 4p = 12 + 32 = 44. Comme la densité est
trois fois le médian, la densité est132.
Problème 4. Une progression arithmétique de neuf éléments
a comme premier nombre 25 et comme dernier 6 1/3. Construisez le carré magique.
Solution. On calcule d’abord la raison p de la
progression arithmétique. Soit a le premier nombre et b le
dernier nombre. Alors, b = a
+ 8p et p = (b – a)/8. D’où, p = -
2 1/3. Le trio est : {(25, 22 2/3, 20 1/3), (18, 15 2/3, 13 1/3), (11, 8
2/3, 6 1/3)}. Le carré magique correspondant est :
|
8 2/3 |
25 |
13 1/3 |
|
20 1/3 |
15 2/3 |
11 |
|
18 |
6 1/3 |
22 2/3 |
|
|
5.08 Trios équivalents
Deux trios sont équivalents si chaque trio contient les mêmes nombres et
si au moins un élément du premier trio prend une autre position dans le
deuxième trio.
Exemple. S = {(6, 9, 12), (4, 7, 10), (2, 5, 8)}
T = {(12, 10, 8), (9, 7, 5), (6, 4, 2)}
S et T sont des trios équivalents.
Tout comme pour le carré magique qu’il engendre, il existe
huit façons différentes de disposer neuf nombres en un trio, soit huit trios
équivalents.
À partir d’un
trio, on peut :
a. intervertir le
premier triplet et le troisième triplet.
b. intervertir le
premier et le troisième élément de chaque triplet.
c. écrire le premier
élément de chaque triplet pour former le premier triplet ; le second
élément pour former le second triplet et le troisième élément pour former
le troisième triplet.
Exemple. Soit T1 = {(2, 4, 6), (5, 7, 9), (8, 10, 12)}
T2 = {(8, 10, 12),
(5, 7, 9), (2, 4, 6)}
T3 = {(6, 4, 2), (9,
7, 5), (12, 10, 8)}
T4 = {(12, 10, 8),
(9, 7, 5), (6, 4, 2)}
T5 = {(2, 5, 8), (4,
7, 10), (6, 9, 12)}
T6 = {(6, 9, 12), (4,
7, 10), (2, 5, 8)}
T7 = {(8, 5, 2), (10,
7, 4), (12, 9, 6)}
T8 = {(12, 9, 6),
(10, 7, 4), (8, 5, 2)}
Les trios équivalents ont les mêmes raisons en valeur
absolue. Le tableau suivant nous indique les raisons en fonction de chaque trio.
|
|
T1 |
T2 |
T3 |
T4 |
T5 |
T6 |
T7 |
T8 |
|
r |
2 |
2 |
- 2 |
- 2 |
3 |
3 |
- 3 |
- 3 |
|
r 0 |
3 |
- 3 |
3 |
- 3 |
2 |
- 2 |
2 |
- 2 |
Le nombre de trios équivalents varie selon le nombre d’éléments
dans l’ensemble associé. Voici un tableau :
|
Éléments |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Trios équivalents |
8 |
0 |
8 |
0 |
4 |
0 |
4 |
0 |
1 |
|
|
5.09 Carré-image
Le carré-image d’ordre 3 est un carré non magique dans lequel chaque
triplet occupe une ligne correspondant à son rang dans le trio. Soit le trio
{(1, 3, 5), (9, 11, 13), (17, 19, 21)}, alors le carré-image est :
Les éléments d’un carré-image peuvent être obtenus
selon le principe de la table d’addition si les nombres sur lesquels on opère
sont en progression arithmétique horizontalement et verticalement. Dans le
carré-image ci-dessous, horizontalement ces nombres sont 4, 7,10 et
verticalement 2, 7, 12.
|
+ |
4 |
7 |
10 |
|
2 |
6 |
9 |
12 |
|
7 |
11 |
14 |
17 |
|
12 |
16 |
19 |
22 |
|
|
On peut aussi utiliser une opération quelconque définie par
des variables du premier degré à la condition que les nombres soient en
progression arithmétique horizontalement ou verticalement. Soit x les
éléments de la première ligne et y les éléments de la première
colonne, l’astérisque est mis pour (3x – 2y). On obtient le
carré-image ci-dessous.
|
* |
4 |
5 |
6 |
|
1 |
10 |
13 |
16 |
|
3 |
6 |
9 |
12 |
|
5 |
2 |
5 |
8 |
|
|
À partir d’un carré-image, on peut obtenir un carré
magique ainsi :
1. On déplace d’une case les éléments périphériques
dans le sens des aiguilles d’une montre.
2. On intervertit les éléments conjugués de la première
colonne, de la deuxième ligne et de la troisième colonne.
Soit le carré-image,
|
5 |
10 |
15 |
|
17 |
22 |
27 |
|
29 |
34 |
39 |
On aura :
|
17 |
5 |
10 |
è
|
34 |
5 |
27 |
|
29 |
22 |
15 |
15 |
22 |
29 |
|
34 |
39 |
27 |
17 |
39 |
10 |
|
Voir Chapitre
6
|
![]()
![]()