|
Série A
Solution 9
La somme des nombres de 1 à 7 est 28. Pour obtenir le maximum,
le nombre central devrait être 7. On fait 28 + 7 = 35 et 35
¸
2 = 17,5. Le nombre maximal par losange devrait alors être 17. Il reste 10 pour
les six autres lunes. On a les combinaisons : (1, 3, 6), (1, 4, 5) et (2,
3, 5), à rejeter à cause de la répétition de nombres. Si le nombre central
est 6, il reste 11 et on a les combinaisons : (1, 3, 7) et (2, 4, 5).
Il peut y avoir au maximum 17 bûcherons dans chaque losange. D’un
côté, on en a 1, 3 et 7 ; de l’autre côté 2, 4 et 5.
Retour
au problème
|
Solution de
l'énigme
CORBEAU
|
|
Série B
Solution 9
On produit un tableau
dans lequel on écrit les nombres donnés horizontalement et verticalement. Les
cases grisées portent un nombre supérieur à 8. Comme deux jetons sont pris à
la fois, les égalités 2 + 7 = 9 et 7 + 2 = 9 sont considérées comme une
seule combinaison.
|
|
1 |
2 |
4 |
5 |
7 |
8 |
|
1 |
|
|
|
|
|
9 |
|
2 |
|
|
|
|
9 |
10 |
|
4 |
|
|
|
9 |
11 |
12 |
|
5 |
|
|
|
|
12 |
13 |
|
7 |
|
|
|
|
|
15 |
|
8 |
|
|
|
|
|
|
Il y a neuf combinaisons dont la somme est supérieure à 8.
Retour
au problème
|
Un angle est une
figure géométrique formée par deux droites qui se rencontrent en un
point commun.
|
|
Série C
Solution 9
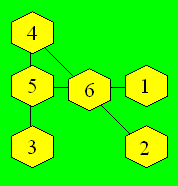
Les combinaisons de trois nombres dont la somme est 12
sont : (1, 5, 6), (2, 4, 6), (3, 4, 5). Le 4 appartient à deux
combinaisons, tout comme le 5 et le 6. Les trois nombres doivent être placés
aux sommets du petit triangle de gauche. Une configuration est :
Retour
au problème
|
Le
premier sablier a été inventé vers l'an 1000. Il était utilisé pour
mesurer des durées courtes.
|
![]()
![]()