*****************
Solutions 151 to 200
*****************
Solution 151. Here are three squares :

Solution 152. We can count six squares.
Solution 153. We can have : (1, 2, 5, 8), (1, 2, 6, 7),
(1, 3, 4, 8), (1, 3, 5, 7), (1, 4, 5, 6), (2, 3, 4, 7), (2, 3, 5, 6). There are
seven groups of four balls.
Solution 154. A = 7 and B = 12.
Solution 155. If we divide each number of the sequence by 4,
the remainder is 3. When we divide a square by 4, the remainder is 1. There is
no square in this sequence.
Solution 156. The expression is : 6 ÷ 2 × 5 - 8.
Solution 157. There are two rectangles : one horizontally (3,
8, 2, 4, 3) and one vertically (2, 4, 7, 4, 3, 5).
Solution 158. As we have a division, it is necessary that the
chosen numbers are divisors of 77. The possible numbers are 7, 11 and 77. The
smallest number is 7.
Solution 159. We can invert 3 and 4, 6 and 9, 10 and 13, 15
and 16.
Solution 160. We remove two segments of the 4 to give 1 and
we move a vertical segment of the 3 to give 2. The smallest number is 12.
Solution 161. An equality is : 17 + 25 + 34 + 68 = 144.
Solution 162. We count six squares 3 ´
3.
Solution 163. The filled grid is :
|
4 |
6 |
5 |
2 |
1 |
3 |
|
1 |
3 |
4 |
6 |
5 |
2 |
|
5 |
2 |
1 |
3 |
4 |
6 |
|
3 |
4 |
6 |
5 |
2 |
1 |
|
6 |
5 |
2 |
1 |
3 |
4 |
|
2 |
1 |
3 |
4 |
6 |
5 |
Solution 164. Sunday
Solution 165. Nine squares 3 ´ 3
Solution 166. The chosen number is 36.
Solution 167. An equality is : 4 × 4 + 4 = 5 × 5 -
5.
Solution 168. There are three years of difference. Peter had
the double of the age of Mary 26 years ago. Peter had then six years and Mary
three years.
Solution 169. Robert will buy 18 stamps of each value.
Solution 170. An arrangement of the numbers is :
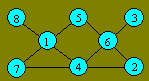
Solution 171. Blondie is 14 years old.
Solution 172. The units are 4, 5 and 6. The tens are 1, 2 and
3. The smallest sum is 75.
Solution 173. We can count 12 squares 3 ´
3.
Solution 174. There was no February 29 in 2001 since the year
is not leap.
Solution 175. This number is 24.
Solution 176. We add 2 a first and a second time ; we
subtract 1. We repeat these operations. The terms of ranks 1, 4, 7, 10 are equal
to their rank. The term of the rank 19 is 19.
Solution 177. We count 25 squares 4 ´
4.
Solution 178. A figure is :

Solution 179. A brick weighs three kilograms. Four bricks
weigh 12 kilograms.
Solution 180. The equality is : 392 + 475 = 867.
Solution 181. We count 10 squares : 9, 36, 81, 144, 225,
324, 441, 576, 729 and 900.
Solution 182. Never. From the 81th floor, Brooke
will not can mount of five floors.
Solution 183. Brice has lived 61 days.
Solution 184. An arrangement of the numbers is :
|
2 |
´ |
3 |
= |
6 |
|
9 |
– |
5 |
= |
4 |
|
1 |
+ |
7 |
= |
8 |
Solution 185. An arrangement of the numbers is :
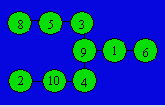
Solution 186. The operations are in order : -
, ¸ , Ö , ´
and +.
Solution 187. The equality is : 246 + 813 + 7 = 1 066.
Solution 188. Two squares : (5, 7, 3, 9) and (9, 2, 5, 7).
Solution 189. Billy possessed 39 balls.
Solution 190. The result is the double of the chosen number.
Solution 191. We add the first two numbers. It is the third number. We subtract 1 to the third number and we repeat these
operations. The
term of the rank 14 is 192.
Solution 192. Benjamin will receive one tocken 1, three
tockens 2 and two tockens 5.
Solution 193. A figure is :

Solution 194. No. For example, we take 7 and 9 : 7 × 9 = 63
and 8 × 8 = 64. We take 11 and 13 : 11 × 13 = 143 and 12 × 12 = 144. The
square is greater of 1.
Solution 195. An arrangement of the balls is :
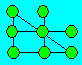
Solution 196. S = 9, B = 7 and R = 5.
Solution 197. We remove the three horizontal segments of the
8. We have 11. The greatest number is 115.
Solution 198. An expression is : (7 ´
100) – (8 ´ 75) + 9.
Solution 199. A figure is :

Solution 200. The last coin is to the rank 5 in relation to
the starting point.
|
![]()
![]()