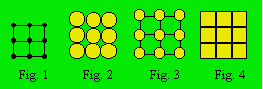
1.0 Notion de treillis
Un treillis est une figure formée par des lignes qui s’entrecroisent et dans lequel les nœuds peuvent contenir des nombres ou des objets. Afin de pouvoir écrire les nombres ou de placer les objets, on dessine notamment des petits cercles ou des petits carrés à la place des nœuds qui sont alors appelés cellules. Un sous-ensemble de cellules accolées ou reliées est appelé rangée. Le treillis de la figure 1 peut être représenté sous les trois autres formes montrées dans les figures 2, 3 et 4.

2.0 Classes de treillis
D’après la disposition des rangées, on peut distinguer quatre classes de treillis :
2.1 Les treillis rectilignes : ceux dont les cellules accolées sont disposées de façon à former des rangées horizontales, verticales ou obliques et ceux dont les cellules sont reliées par des segments de droite. Ces rangées sont dites rectilignes. Le treillis de la figure 5 contient six rangées de trois cellules chacune : trois horizontales et trois verticales. On pourrait ajouter deux rangées diagonales si on reliait les cellules par une droite.

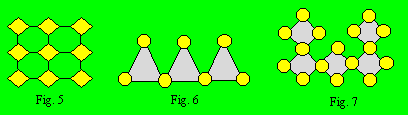
2.2 Les treillis polygonaux : ceux dont les cellules sont reliées par des segments formant des polygones généralement congruents qui constituent les rangées. Dans le treillis de la figure 6, les trois rangées de trois cellules chacune sont constituées par des triangles grisés. Le treillis de la figure 7 contient cinq rangées de quatre cellules correspondant aux cinq losanges grisés. On marque les polygones pour indiquer la place des rangées ou on l’exprime par des mots. Ces rangées sont dites polygonales.

2.3 Les treillis curvilignes : ceux dont les cellules sont reliées par des arcs de cercles ou par des courbes fermées. Le treillis de la figure 8 contient quatre rangées de quatre cellules chacune, celui de la figure 9 trois rangées de trois cellules chacune. Ces rangées sont dites curvilignes.

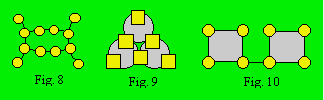
2.4 Les treillis mixtes : ceux qui ont les propriétés d’au moins deux treillis définis précédemment. Il peut arriver que la forme d’un treillis mixte soit identique à un treillis rectiligne, polygonal ou curviligne. Ce sont des informations additionnelles concernant les rangées qui vont préciser la classe du treillis. Le treillis de la figure 10 est polygonal si on considère seulement les carrés pour définir les rangées. Il est mixte si on considère une troisième rangée, soit le segment de la base qui supporte quatre cellules. Les rangées de ces treillis peuvent être rectilignes, polygonales ou curvilignes.

3.0 Treillis harmonieux
Un treillis est dit harmonieux quand toutes les rangées ont le même nombre de cellules. Le treillis rectiligne de la figure 11 est harmonieux si on s’en tient aux rangées indiquées par des pointillés. Il comporte sept rangées de trois cellules : trois horizontales et quatre verticales. On pourrait ajouter des diagonales de trois cellules et il serait encore harmonieux. Le treillis polygonal de la figure 12 n’est pas harmonieux. Il contient deux triangles de trois cellules et un de quatre cellules.

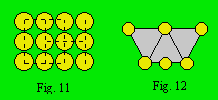
L’ordre d’un treillis est le nombre de cellules par rangée. Le treillis harmonieux qui a trois cellules par rangée est d’ordre 3. Lorsque le treillis n’est pas harmonieux, l’ordre est multiple. Le treillis de la figure 12 est d’ordre (3, 4).

4.0 Classification des treillis
Afin de pouvoir identifier chaque treillis, on leur attribue un code et un sous-code.

4.1 Code attribué à un treillis
Le code est constitué de cinq paramètres sous la forme : A-B-C-D-E où A est le nombre de cellules du treillis, B le nombre de rangées, C le nombre de cellules par rangée ou ordre du treillis, D le degré des cellules, E le compteur de différenciation. Pour le treillis de la figure ci-dessous, A = 9, B = 8 et C = 3. Pour établir le paramètre D, nous allons d’abord définir le degré.

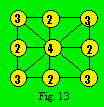
Le degré d’une cellule correspond au nombre de rangées qui passent par cette cellule. La figure 13 montre le degré de chaque cellule. Quatre cellules sont de degré 2, quatre de degré 3 et une de degré 4. Nous allons condenser cette information en un nombre dont l’unité représente le nombre de cellules qui sont de degré 1, la dizaine le nombre de cellules de degré 2, la centaine le nombre de cellules de degré 3, l’unité de mille le nombre de cellules de degré 4 et ainsi de suite. Le paramètre D de la figure 13 est 1440. Notons que la somme des "chiffres" du paramètre D doit être égale au paramètre A. Lorsque le nombre de cellules est plus grand que 9, on souligne tout nombre excédant 9.

Le cinquième paramètre est un compteur qui permet de lister les treillis et de les différencier. Nous expliquerons un peu plus loin comment déterminer le compteur. Le code du treillis de la figure 13, sauf le compteur, est : 9-8-3-1440. Nous considérons que deux treillis ont le même code quand les quatre premiers paramètres sont identiques.

4.2 Sous-code attribué à un treillis
Le sous-code est formé de n-uplets dont les éléments sont les degrés des cellules. On forme un n-uplet pour chaque rangée. L’ordre de lecture sur le treillis se fait de gauche et à droite et de haut en bas. Le treillis de la figure 14 contient cinq triplets : (1, 2, 3), (2, 2, 2), (2, 2, 2), (1, 2, 3), (2, 3, 2). On écrira en abrégé : 2 × (1, 2, 3), 2 × (2, 2, 2) et 1 × (2, 3, 2), c’est le sous-code. Notons que le nombre de n-uplets est égal au paramètre B et le nombre d’éléments dans chaque n-uplet au paramètre C.

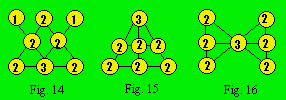
Les treillis 15 et 16 ont le même code et un sous-code différent. Le code des deux treillis est : 7-5- 3-160. Le sous-code du premier est : 2 × (2, 2, 2), 3 × (3, 2, 2). Le sous-code du second est : 2 × (2, 2, 2), 3 × (2, 3, 2). Deux treillis ayant le même code sont différents lorsqu’au moins un n-uplet du sous-code est différent ou encore lorsqu’au moins un élément n’est pas dans la même position dans un n-uplet d’un sous-code à l’autre.

5.0 Treillis isomorphes
Deux treillis sont isomorphes quand ils ont le même code et le même sous-code. Les treillis 17 et 18 sont isomorphes. Leur code est 5-2-3-14. Leur sous-code est : 2 × (1, 2, 1).

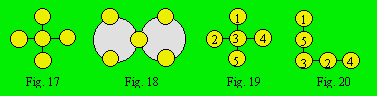
Deux treillis magiques isomorphes utilisent les mêmes combinaisons de nombres et les nombres apparaissent dans le même ordre sur les rangées. Le code des deux treillis 19 et 20 est 5-2-3-14. Le sous-code du premier est 2 × (1, 2, 1). Le sous-code du second est 2 × (1, 1, 2). Les deux treillis ne sont pas isomorphes.

Le compteur est conçu pour classer les treillis isomorphes. La valeur du paramètre est relative, parce qu’elle peut être différente d’une personne à l’autre. Le premier treillis trouvé par une personne reçoit "1a" comme compteur. Si le deuxième treillis trouvé n’est pas isomorphe, on le désigne par "2a", le troisième par "3a" et ainsi de suite. Si le deuxième treillis trouvé est isomorphe à "1a", on le désigne par "1b", le troisième par "1c" et ainsi de suite.

6.0 Magie d’un treillis
Un treillis d’ordre n est magique quand des nombres sont disposés dans les cellules de telle manière que la somme soit la même dans chaque rangée. Cette somme est appelée densité du treillis magique. Par ailleurs, la disposition des nombres dans le treillis constitue une configuration.

Le treillis de la figure 21 comporte huit rangées et neuf cellules. Son ordre est 3 et sa densité 15. Celui de la figure 22 possède trois rangées et sept cellules. Son ordre est 3 et sa densité 13.

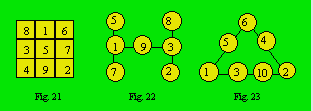
Un treillis d’ordre multiple est magique quand la somme des nombres de chaque rangée est proportionnelle au nombre de cellules par rangée. Le treillis de la figure 23 a trois rangées et sept cellules. Il est d’ordre (3, 4). La somme est 12 pour les rangées de trois cellules et de 16 pour la rangée de quatre cellules. La densité est (12, 16) : ce qui fait un rapport de 3 à 4, comme pour l’ordre du treillis.

Un treillis magique est normal quand il est constitué des entiers consécutifs différents à partir de 1’unité jusqu’au nombre de cellules. Le treillis magique de la figure 21 est normal ; ceux des figures 22 et 23 ne le sont pas.

7.0 Densité des treillis magiques harmonieux et normaux
La densité d’un carré magique d’ordre n est unique. Elle correspond à un seul nombre. Ce carré magique d’ordre 4 (fig. 24) a une densité de 34. Il existe 880 configurations différentes.

Nous allons maintenant nous attarder à la formation des treillis magiques harmonieux qui sont normaux. Définissons d’abord la densité probable et la densité possible. La densité probable est celle qui s’applique à tous les treillis ayant le même nombre de cellules. La densité possible constitue un sous-ensemble des densités probables et s’applique à un treillis donné. Une densité probable peut devenir possible ; une densité possible peut engendrer des configurations ou pas.

7.1 Densités probables des treillis magiques harmonieux et normaux
La plus petite densité probable d’un treillis normal d’ordre n ayant m cellules correspond à la somme de n entiers : les (n - 1) plus petits et le plus grand, soit m. Ainsi, la plus petite densité probable d’un treillis d’ordre 4 comprenant 12 cellules est : 1 + 2 + 3 + 12 = 18.

La plus grande densité probable d’un treillis normal d’ordre n ayant m cellules correspond à la somme de n entiers : le plus petit, soit 1, et les (n - 1) plus grands. Ainsi, la plus grande densité probable d’un treillis d’ordre 4 comprenant 12 cellules est : 1 + 10 + 11 + 12 = 34. La plus petite densité probable du treillis de la figure 25 est 18 et la plus grande est 34.

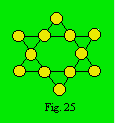
Tous les nombres compris entre la plus petite et la plus grande densité sont également des densités probables. Le tableau suivant indique les densités probables pour des treillis d’ordres 2 à 5 ayant de 4 à 16 cellules.

Nous pouvons établir les généralités suivantes, lorsque m est plus grand ou égal à  n :
1. La plus petite densité probable d’un treillis harmonieux normal d’ordre n plus grand ou égal à 2 est égale à m + T(n - 1) où T est un nombre triangulaire ou encore est égale à m + [n(n - 1)/2].

2. La plus grande densité probable d’un treillis d’ordre n plus grand ou égal à 2 est égale à m(n - 1) - T(n - 2) + 1 où T est un nombre triangulaire ou encore est égale à m(n - 1) - [n(n - 3)/2].

3. Le nombre de densités probables est égal à (m - n)(n - 2) + 1.

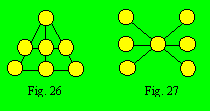
Les treillis des figures 26 et 27 ont sept cellules chacune et sont d’ordre 3. La plus petite densité probable de ces deux treillis est 10 et la plus grande est 14. Les densités probables sont 10, 11, 12, 13 et 14.

7.2 Densités possibles des treillis magiques harmonieux et normaux
Un treillis donné n’admet pas nécessairement toutes les densités probables. Pour former un treillis magique, il faut d’abord établir les densités pour lesquelles il semble possible de trouver au moins une configuration : ce sont les densités possibles. Pour connaître les densités possibles, il faut d’abord calculer la somme indexée. C’est une somme qui tient compte de la position d’un nombre dans le treillis et du degré de la cellule où il est. Cette somme indexée S_i est la somme des résultats obtenus en multipliant chaque élément d’une cellule par son degré.

La somme indexée S_i du treillis de la figure 28 est : (1 × 2) + (2 × 2) + (3 × 2) + (4 × 3) + (5 × 2) + (6 × 2) + (7 × 2) = 60. En abrégé, on peut écrire : S_i = 2(1 + 2 + 3 + 5 + 6 + 7) + 3 × 4 = 60. Si on divise ce résultat par le nombre de rangées, soit 5, on obtient bien 12 qui est la densité.

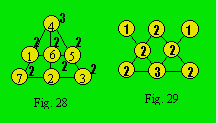
Quand on doit disposer des nombres dans un treillis, on cherche d’abord la plus petite densité possible. Dans le treillis de la figure 29, une cellule est de degré 3, cinq sont de degré 2 et deux de degré 1.

On trouve la plus petite densité possible. La plus petite somme indexée sera égale à la somme des résultats suivants :

le plus petit nombre, soit 1, multiplié par 3 : 1 × 3 = 3

la somme des cinq entiers consécutifs suivants (2, 3, 4, 5, 6) multipliée par 2 : 20 × 2 = 40

la somme des deux entiers consécutifs suivants (7, 8) multipliée par 1 : 15 × 1 = 15

La somme de ces résultats est 58. On compte cinq rangées. La plus petite densité possible est 58/5 = 11,6. On choisit la plus petite valeur entière supérieure à 11,6 : c’est 12. Si on se réfère au tableau précédent, la plus petite densité probable était 11. Maintenant, on est assuré que 11 ne peut pas engendrer une configuration pour ce treillis.

On cherche la plus grande densité possible. La plus grande somme indexée sera égale à la somme des résultats suivants :

le plus grand nombre, soit 8, multiplié par 3 : 8 × 3 = 24

la somme des cinq entiers consécutifs suivants en ordre décroissant (7, 6, 5, 4, 3) multipliée par 2 : 25 × 2 = 50

la somme des deux entiers consécutifs suivants en ordre décroissant (2, 1) multipliée par 1 : 3 × 1 = 3

La somme de ces résultats est 77. On compte cinq rangées. La plus grande densité possible est 77/5 = 15,4. On choisit la plus grande valeur entière inférieure à 15,4 : c’est 15. Si on se réfère au tableau précédent, la plus grande densité probable était 16. Elle est donc maintenant exclue pour ce treillis. En résumé, les densités possibles de ce treillis sont 12, 13, 14 et 15.

7.3 Densités complémentaires des treillis magiques harmonieux et normaux
Lorsqu’il y a plus d’une densité pour un treillis, la plus petite densité possible d₁ et la plus grande densité possible d₂ sont dites complémentaires. Il en est de toute paire de densités dont la somme est : d₁ + d₂. Ainsi, dans le treillis de la figure 29, 12 et 15 sont des densités complémentaires, de même que 13 et 14.

Connaissant la plus petite densité d₁ et la plus grande d₂, on peut trouver la complémentaire d’une densité d₃ dans l’intervalle des densités possibles en appliquant la formule : d₁ + d₂ - d₃. Si on ne connaît pas les densités d₁ et d₂, la complémentaire de d₃ est : n(m + 1) - d₃, où n est l’ordre et m le nombre de cellules.

Par exemple, connaissant la densité 13 dans le treillis de la figure 29, la densité complémentaire est : 3(8 + 1) - 13 = 14. Il est possible que le résultat obtenu soit égal à d₃. Dans ce cas, la densité donnée n’a pas de complémentaire. C’est une densité unique ou la densité centrale de celles qui sont possibles. Ainsi, dans un treillis de huit cellules d’ordre 4, la densité centrale est 18. De façon générale, la densité centrale est égale à n(m + 1)/2. Si le résultat n’est pas un nombre entier, il n’y a pas de densité centrale.

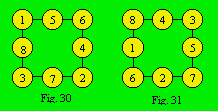
Lorsque les densités sont complémentaires, les treillis sont également dits complémentaires. Connaissant une configuration d’un treillis avec une densité déterminée, on peut former le treillis complémentaire en soustrayant tout élément de (m + 1). La densité du treillis de la figure 30 est 12 ; celle de la figure 31 est 15. Les deux densités sont complémentaires et les treillis aussi sont complémentaires.

Dans la recherche pour former des treillis magiques, on peut partir de la plus petite densité jusqu’à la densité centrale. Si on a besoin de connaître les configurations pour les autres densités, on utilise cette règle de formation des treillis complémentaires.

8.0 Formation des treillis magiques harmonieux et normaux
La prochaine étape consiste à vérifier si chacune des densités possibles permet des configurations ou non. Il existe plusieurs procédés de formation de treillis magiques. Nous en expliciterons un à partir des combinaisons.

8.1 Code attribué aux combinaisons
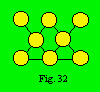
Connaissant la densité 12 du treillis de la figure 32, nous allons rechercher toutes les combinaisons de trois nombres choisis parmi les entiers de 1 à 8 dont la somme est 12. Il y en a six. Les voici : (1, 3, 8), (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6) et (3, 4, 5).

Nous devons comparer le nombre de combinaisons avec le nombre de rangées. S’il y a moins de combinaisons que de rangées, il n’y a pas de configuration. Tel n’est pas le cas ici.

On détermine la fréquence d’apparition de chaque nombre dans les combinaisons. La fréquence de 1, qui est notée f(1), est 3, puisque le 3 apparaît trois fois. Voici le détail des fréquences : f(1) = 3, f(2) = 2, f(3) = 3, f(4) = 3, f(5) = 2, f(6) = 2, f(7) = 2 et f(8) = 1. Trois nombres (1, 3, 4) apparaissent trois fois, quatre nombres (2, 5, 6, 7) deux fois et un nombre (8) une fois.

La somme des fréquences est 18. Ce qui est exact puisqu’on a puisé les informations dans six combinaisons de trois nombres chacun. Tout comme on l’a fait pour le treillis, on attribue un code à chaque ensemble de combinaisons. Ce code est aussi constitué de cinq paramètres sous cette forme : A-B-C-D-E où A est le plus grand entier, B le nombre de combinaisons, C le nombre d’éléments par combinaison, D la fréquence des éléments, E la somme des éléments de chaque combinaison.

Pour le treillis de la figure 32, le code des combinaisons est 8-6-3-341-12. Le paramètre 341 signifie que, dans les combinaisons, trois nombres apparaissent trois fois (centaine), quatre nombres deux fois (dizaine) et un nombre une seule fois (unité). Le cinquième paramètre remplace le compteur retenu dans le code du treillis.

8.2 Disposition des nombres selon leur fréquence
Le code du treillis de la figure 32 est 8-5-3-152-1a et celui des combinaisons est 8-6-3-341-12. Les deux premiers paramètres sont identiques. Le troisième paramètre est supérieur de 1 dans les combinaisons. D’où, une combinaison ne servira pas. Le quatrième paramètre du code des combinaisons est supérieur. D’où, un seul des trois nombres de fréquence 3 peut apparaître dans la cellule de degré 3. Dans les cinq cellules de degré 2, on pourra placer cinq nombres parmi les deux nombres non choisis de fréquence 3 et les quatre de fréquence 2. Dans les deux cellules de degré 1, on devra placer le nombre de fréquence 1 et un des nombres qui restent.

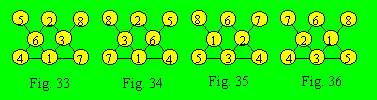
La cellule centrale de la base recevra 1, 3 ou 4, car ces trois éléments ont une fréquence de 3 dans les combinaisons. L’une des cellules supérieures des extrémités recevra 8. En appliquant ces données et avec un peu de tâtonnement, on trouve les quatre configurations suivantes quand la densité est 12.

Les configurations 33 et 34 sont considérées comme équivalentes. On peut tracer un axe de symétrie vertical passant par le centre de la figure : 8 est l’image de 5 ; 3 est l’image de 6 ; 7 est l’image de 4. Les configurations 35 et 36 sont aussi équivalentes à cause d’un même axe de symétrie. Ce treillis a donc deux configurations quand la densité est 12.

Si la densité est 13, les combinaisons sont : (1, 4, 8), (1, 5, 7), (2, 3, 8), (2, 4, 7), (2, 5, 6) et (3, 4, 6). La fréquence de chaque nombre dans les combinaisons est : f(1) = 2, f(2) = 3, f(3) = 2, f(4) = 3, f(5) = 2, f(6) = 2, f(7) = 2, f(8) = 2. Deux nombres (2, 4) apparaissent trois fois et six nombres (1, 3, 5, 6, 7, 8) deux fois.

Le code des combinaisons est : 8-6-3-260-13. La comparaison avec le code du treillis qui est 8-5-3-152-1a permet de croire que des configurations sont possibles. La cellule centrale de la base recevra 2 ou 4. Après avoir placé 2, on complète les rangées avec 3 et 8, 4 et 7, puis 5 et 6. Après avoir placé 4, on complète avec 1 et 8, 2 et 7, ou 3 et 6. En appliquant ces données et avec un peu de tâtonnement, on trouve les configurations 37 et 38.

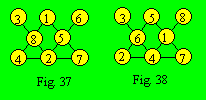
En déplaçant les éléments par rapport à un axe de symétrie verticale, on obtiendrait, dans chaque cas, une configuration équivalente.

La densité 14 est complémentaire à la densité 13. Il y a donc deux configurations pour la densité 14 (fig. 39 et 40). Ce sont les complémentaires des treillis des figures 37 et 38.

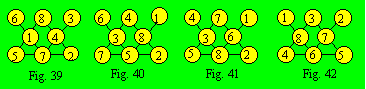
La densité 15 est complémentaire à la densité 12. Dans ce cas, le treillis a deux configurations (fig. 41 et 42). Ce sont les complémentaires des treillis des figures 33 et 35. Bref, le treillis de la figure 32 a en tout six configurations différentes quand on place les entiers consécutifs de 1 à 8.

9.0 En guise de conclusion
Nous vous avons présenté un procédé pour construire des treillis magiques. Ce procédé peut s’appliquer à tous les treillis. Quand l’ordre du treillis est relativement grand, le travail de recherche peut être plus long. C’est alors l’occasion d’associer d’autres stratégies.

La démarche proposée permet donc une économie de temps et permet surtout d’identifier assez rapidement s’il y a configuration ou pas. Lorsqu’un treillis ne peut pas être magique et qu’on procède par tâtonnement, on ne peut pas déclarer qu’il n’y a pas de configuration, à moins d’avoir vérifié toutes les combinaisons. Avec un peu de pratique et en appliquant le procédé expliqué, certains treillis peuvent être résolus rapidement. Û

______
Références sur les carrés magiques
Ball, W. W. & Coxeter, H. S. (1974). Magic Squares. Dans Mathematical Recreations and Essays. Toronto, University of Toronto, p. 193-221.

Benson, W. & Jacoby, O. (1976). New Recreations With Magic Squares. New York, Dover.

Ducret, Étienne. (1980). Les carrés magiques. Dans Divertissements mathématiques. Paris, Garnier, p. 130-142.

Fourrey, E.(1947). Les carrés magiques. Dans Récréations arithmétiques. Paris, Vuibert, p. 197-261.

Gardner, Martin. (1964). Le carré magique. Dans Problèmes et divertissements mathématiques, tome 1. Paris, Dunod, p. 13-20.

Gardner, Martin. (1965). Les carrés magiques. Dans Problèmes et divertissements mathématiques, no 2. Paris, Dunod, p. 111-120.

Jean, Charles-É. (1981). Initiation aux carrés magiques. Québec, MÉQ.

Kordiemsky, Boris. (1963). Sommes croisées et carrés magiques. Dans Sur le sentier des mathématiques, tome 2. Paris, Dunod, p. 31-69.

Kraitchik, Maurice. (1953). Magic Squares. Dans Mathematical Recreations. New York, Dover, p. 142-192.

Lucas, Édouard.(1960). Les carrés magiques de Fermat. Dans Récréations mathématiques, tome 4. Paris, Blanchard, p. 89-121.

Moran, Jim. (1982). The Wonders of Magic Squares. New York, Vintage.

Pérelman, Y. (1974). Les carrés magiques. Dans Expériences et problèmes récréatifs. Moscou, Mir, p. 436-450.

Simon, William. (1993). Magic Squares. Dans Mathematical Magic. New York, Dover, p. 106-134.