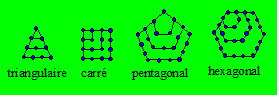
Un nombre polygonal est un nombre qui peut être représenté par un polygone régulier constitué de points disposés de façon symétrique. Voici quatre ordres de polygonaux :

Un même nombre peut appartenir à plusieurs ordres de polygonaux.

La notion de suite arithmétique joue un rôle important dans l’existence de ces nombres. En effet, ceux-ci sont formés par l’addition des éléments d’une suite toujours à partir de 1. Voici la distribution pour les cinq plus petits nombres polygonaux d’ordres 3 à 6 :

Nombres triangulaires ou d’ordre 3 : suite de raison 1

Nombres carrés ou d’ordre 4 : suite de raison 2

Nombres pentagonaux ou d’ordre 5 : suite de raison 3

Nombres hexagonaux ou d’ordre 6 : suite de raison 4

Par exemple, pour les nombres hectogonaux ou polygonaux d’ordre 100, le premier nombre est 1, le deuxième 100 et la raison 98. On aura donc la suite : 1, 100, 297, 592, 985, etc.

Dans cet article, nous allons montrer comment trouver des égalités de polygonaux de tous les ordres. Nous adoptons des symboles comme exposants des polygonaux traités : Δ pour les triangulaires, p pour les pentagonaux, h pour les hexagonaux, s pour les heptagonaux, o pour les octogonaux. Par exemple, 14^p se lit 14 pentagonal ou pentagonal de rang 14. Sa valeur est 287. On peut écrire : 14^p = 287.

Voici les sujets à partir desquels on peut trouver des égalités sans trop de calculs:

1. Un carré magique d’ordre 3

2. Deux carrés magiques d’ordre 3

3. Un carré magique d’ordre 4

4. Sommes des bases de deux polygonaux

5. Sommes combinées des bases de deux polygonaux

6. Deux suites

7. Expressions algébriques

8. Fraction d’une somme

9. Opérations de transformation

1. Un carré magique d’ordre 3

Soit le carré magique suivant dans lequel on considère chaque nombre comme étant le rang d’un polygonal :

Par exemple, sur la première ligne, on a le pentagonal de rang 10, le pentagonal de rang 1, le pentagonal de rang 7. En abrégeant, on peut écrire : 10^p = 145, 1^p = 1, 7^p = 70. La somme des pentagonaux est 216.

Égalités de six polygonaux du même ordre

Dans tout carré magique 3 × 3, la somme des polygonaux d’un ordre donné est la même dans la première et la troisième ligne. Il en est ainsi pour la première et la troisième colonne.

Voici des égalités qui découlent de cette proposition à partir du carré magique donné :

a) Triangulaires où est Δ est l’exposant

10^Δ + 1^Δ + 7^Δ = 5^Δ + 11^Δ + 2^Δ = 84

10^Δ + 3^Δ + 5^Δ = 7^Δ + 9^Δ + 2^Δ = 76

b) Carrés où 2 est l’exposant

10² + 1² + 7² = 5² + 11² + 2² = 150

10² + 3² + 5² = 7² + 9² + 2² = 134

c) Pentagonaux où p est l’exposant

10^P + 1^P + 7^P = 5^P + 11^P + 2^P = 216

10^P + 3^P + 5^P = 7^P + 9^P + 2^P = 192

Toutes ces égalités sont vraies pour les polygonaux de tout ordre.

Égalité de 12 polygonaux du même ordre

Considérons le même carré magique d’ordre 3. Écrivons sous forme d’égalité les nombres de la première et de la troisième ligne.

10 + 1 + 7 = 5 + 11 + 2 = 18

On prend un nombre qui est supérieur au plus grand nombre de cette égalité, ordinairement le suivant. On l’appelle l’opérateur. Dans ce cas-ci, on peut choisir 12. De l’opérateur, on soustrait chacun des nombres de l’égalité, puis on leur additionne l’opérateur. On obtient :

2 + 22 + 11 + 13 + 5 + 19 = 7 + 17 + 1 + 23 + 10 + 14 = 72

En considérant les heptagonaux dont l’exposant est s et tout en respectant l’ordre numérique, on peut écrire :

2^s + 5^s + 11^s + 13^s + 19^s + 22^s = 1^s + 7^s + 10^s + 14^s + 17^s + 23^s = 2802

Cette égalité est vraie pour les polygonaux de tout ordre. Cela s’applique aussi aux cubes.

2³ + 5³ + 11³ + 13³ + 19³ + 22³ = 1³ + 7³ + 10³ + 14³ + 17³ + 23³ = 21 168

Égalité de 24 polygonaux du même ordre

En suivant les mêmes règles et en partant de l’égalité précédente, on peut trouver une égalité de 24 termes. Comme 23 est la plus grande base, on choisit 24 comme opérateur.

En considérant les hexagonaux et en respectant l’ordre numérique, on peut écrire :

2^h + 5^h + 11^h + 13^h + 19^h + 22^h + 26^h + 29^h + 35^h + 37^h + 43^h + 46^h = 1^h + 7^h + 10^h + 14^h + 17^h + 23^h + 25^h + 31^h + 34^h + 38^h + 41^h + 47^h = 18 192

Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

2³ + 5³ + 11³ + 13³ + 19³ + 22³ + 26³ + 29³ + 35³ + 37³ + 43³ + 46³ = 1³ + 7³ + 10³ + 14³ + 17³ + 23³ + 25³ + 31³ + 34³ + 38³ + 41³ + 47³ = 333 504

2. Deux carrés magiques d’ordre 3

Prenons deux carrés magiques qui n’ont aucun lien entre eux.

Égalité de 12 polygonaux du même ordre

La proposition précédente permet de réunir les éléments de certaines rangées :

• Ligne 1 du carré 1 + ligne 1 du carré 2 = ligne 3 du carré 1 + ligne 3 du carré 2

• Ligne 1 du carré 1 + ligne 3 du carré 2 = ligne 3 du carré 1 + ligne 1 du carré 2

• Colonne 1 du carré 1 + colonne 1 du carré 2 = colonne 3 du carré 1 + colonne 3 du carré 2

• Colonne 1 du carré 1 + colonne 3 du carré 2 = colonne 3 du carré 1 + colonne 1 du carré 2

En considérant les triangulaires et en respectant l’ordre numérique, on peut écrire par rapport aux lignes 1 et 3 :

1^Δ + 7^Δ + 10^Δ + 13^Δ + 16^Δ + 22^Δ = 2^Δ + 5^Δ + 11^Δ + 12^Δ + 18^Δ + 21^Δ = 564

Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

1³ + 7³ + 10³ + 13³ + 16³ + 22³ = 2³ + 5³ + 11³ + 12³ + 18³ + 21³ = 18 285

Pour obtenir des égalités comprenant un plus grand nombre de termes, on peut utiliser autant de carrés magiques que l’on veut. Toutefois, s’il y a des doublons de part et d’autre de l’égalité, on les biffe.

3. Un carré magique d’ordre 4

Le carré magique général qui suit est formé de trois variables. La somme de chacune des huit rangées est 4a + 6b + 6c.

En faisant les calculs appropriés, on peut établir les propositions suivantes :

• La somme des polygonaux d’un même ordre de la première ligne est égale à la somme de ceux de la quatrième ligne.

• La somme des polygonaux d’un même ordre de la deuxième ligne est égale à la somme de ceux de la troisième ligne.

• La somme des polygonaux d’un même ordre de la première colonne est égale à la somme de ceux de la quatrième colonne.

• La somme des polygonaux d’un même ordre de la deuxième colonne est égale à la somme de ceux de la troisième colonne.

Égalité de huit polygonaux du même ordre

Pour trouver des égalités de polygonaux, on donne une valeur à chaque variable. On forme ainsi un carré magique. On applique l’une ou l’autre des propositions précédentes.

Exemple. On fait a = 1, b = 2 et c = 5. On obtient le carré magique ci-après dont la somme par rangée est 46.

En considérant les pentagonaux en ordre numérique et par rapport aux lignes 1 et 4, on peut écrire :

3^p + 5^p + 16^p + 22^p = 1^p + 7^p + 18^p + 20^p = 1138

Cette égalité vaut pour les nombres polygonaux de tout ordre.

Égalité de 16 polygonaux du même ordre

Appliquons la stratégie de l’opérateur sur l’égalité précédente. On choisit 23 comme opérateur. On peut écrire en ordre numérique :

1^s + 7^s + 18^s + 20^s + 26^s + 28^s + 39^s + 45^s = 3^s + 5^s + 16^s + 22^s + 24^s + 30^s + 41^s + 43^s = 14 174

Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

1³ + 7³ + 18³ + 20³ + 26³ + 28³ + 39³ + 45³ = 3³ + 5³ + 16³ + 22³ + 24³ + 30³ + 41³ + 43³ = 204 148

4. Sommes des bases de deux polygonaux

On choisit un nombre qui sera la somme des bases. On établit la somme de tous les couples de triangulaires dont la somme des bases est ce nombre. Par exemple, on choisit 19.

Égalités de huit polygonaux du même ordre

On recherche deux sommes dont la somme est la même que celle d’un autre couple de sommes. Dans ce cas-ci, les possibilités sont :

172 + 100 = 142 + 130 = 272

156 + 106 = 142 + 120 = 262

142 + 100 = 130 + 112 = 242

130 + 102 = 120 + 112 = 232

On écrit les deux éléments qui composent chaque somme. Voici l’égalité pour chaque possibilité en considérant les carrés :

1² + 9² + 10² + 18² = 3² + 4² + 15² + 16² = 506

2² + 7² + 12² + 17² = 3² + 5² + 14² + 16² = 486

3² + 9² + 10² + 16² = 4² + 6² + 13² + 15² = 446

4² + 8² + 11² + 15² = 5² + 6² + 13² + 14² = 426

Ces égalités valent pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

1³ + 9³ + 10³ + 18³ = 3³ + 4³ + 15³ + 16³ = 7562

Égalité de 12 polygonaux du même ordre

Dans le tableau précédent, on recherche trois sommes dont la somme est la même que celle d’un autre triplet de sommes.

Par exemple, on écrit : 172 + 106 + 100 = 156 + 120 + 102 = 378. Voici l’égalité en considérant les nombres pentagonaux :

1^P + 7^P + 9^P + 10^P + 12^P + 18^P = 2^P + 5^P + 8^P + 11^P + 14^P + 17^P = 1020

Cette égalité est vraie pour les polygonaux de tout ordre. Elle s’applique aussi aux cubes.

1³ + 7³ + 9³ + 10³ + 12³ + 18³ = 2³ + 5³ + 8³ + 11³ + 14³ + 17³ = 9633

Égalité de 16 polygonaux du même ordre

Dans le tableau précédent, on recherche quatre sommes dont la somme est la même que celle d’un autre quadruplet de sommes.

Par exemple, on écrit : 172 + 130 + 106 + 102 = 156 + 142 + 112 + 100 = 510. Voici l’égalité en considérant les triangulaires :

1^Δ + 4^Δ + 7^Δ + 8^Δ + 11^Δ + 12^Δ + 15^Δ + 18^Δ = 2^Δ + 3^Δ + 6^Δ + 9^Δ + 10^Δ + 13^Δ + 16^Δ + 17^Δ = 510

Cette égalité est vraie pour les polygonaux de tout ordre. Elle s’applique aussi aux cubes.

1³ + 4³ + 7³ + 8³ + 11³ + 12³ + 15³ + 18³ = 2³ + 3³ + 6³ + 9³ + 10³ + 13³ + 16³ + 17³ = 13 186

5. Sommes combinées des bases de deux polygonaux

On choisit deux nombres qui seront la somme de bases. Pour chacun, on établit la somme de tous les couples de triangulaires. Par exemple, on choisit 9 et 13.

Égalité de six polygonaux du même ordre

À partir du tableau, on peut écrire : 37 + 49 = 31 + 55. On écrit les deux éléments qui composent chaque somme. Voici une égalité en considérant les pentagonaux :

1^P + 8^P + 6^P + 7^P = 2^P + 7^P + 4^P + 9^P = 214

On biffe 7^P de part et d’autre. L’égalité est :

1^P + 6^P + 8^P = 2^P + 4^P + 9^P = 144

Cette égalité est vraie pour les polygonaux de tout ordre.

Égalité de huit polygonaux du même ordre

À partir du même tableau, on peut écrire : 37 + 49 = 25 + 61. On écrit les deux éléments qui composent chaque somme.

1^Δ + 8^Δ + 6^Δ + 7^Δ = 4^Δ + 5^Δ + 3^Δ + 10^Δ = 86

En considérant les heptagonaux, on a l’égalité :

1^S + 6^S + 7^S + 8^S = 3^S + 4^S + 5^S + 10^S = 342

Cette égalité est vraie pour les polygonaux de tout ordre.

6. Deux suites

Sur la première ligne, on écrit une suite de quatre nombres. On choisit un nombre qu’on additionne à chacun des termes précédents. Voici deux suites :

Égalité de huit polygonaux du même ordre

Le premier membre de l’égalité peut être formé par les nombres des cases colorées. Le deuxième membre l’est alors par les quatre autres nombres. En considérant les carrés, on peut écrire en ordre numérique :

5² + 10² + 11² + 12² = 7² + 8² + 9² + 14² = 390

Cette égalité est vraie pour les polygonaux de tout ordre.

 Égalité de 16 polygonaux du même ordre

On écrit sur la première ligne les nombres de 2 à 9. La raison est 1. Par exemple, on additionne 8 à ces nombres : ce qui donne une seconde suite dont la raison est encore 1.

On applique le procédé précédent dans chaque section de huit cases définis par un séparateur. Le premier membre de l’égalité peut être formé par les nombres des cases colorées. Le deuxième membre l’est alors par les autres nombres.

En considérant les hexagonaux, on peut écrire en ordre numérique :

2^h + 5^h + 6^h + 9^h + 11^h + 12^h + 15^h + 16^h = 3^h + 4^h + 7^h + 8^h + 10^h + 13^h + 14^h + 17^h = 1708

Cette égalité est vraie pour les polygonaux de tout ordre.

Si on veut obtenir une égalité qui contient les nombres de 1 à 16, on peut utiliser ce tableau.

7. Expressions algébriques

On veut former des égalités de polygonaux à partir d’expressions algébriques. Les valeurs de (ad – bc) et (bd + ac) seront utilisées pour le premier membre. Les valeurs de (ad + bc) et (bd – ac) le seront pour l’autre membre.

Égalité de huit polygonaux du même ordre

Par exemple, a = 1, b = 3, c = 1 et d = 4. En remplaçant chaque expression algébrique par sa valeur numérique, on obtient 1 et 13, puis 7 et 11. On choisit un nombre supérieur au plus grand qu’on appelle opérateur. Allons-y pour 14. Pour chaque nombre précédent, on soustrait de 14 et on additionne 14. On obtient :

13 + 15 + 1 + 27 = 7 + 21 + 3 + 25 = 56

Pour les octogonaux dont l’exposant est o, on peut écrire tout en respectant l’ordre numérique :

1^o + 13^o + 15^o + 27^o = 3^o + 7^o + 21^o + 25^o = 3260

Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

1³ + 13³ + 15³ + 27³ = 3³ + 7³ + 21³ + 25³ = 25 256

Égalité de 16 polygonaux du même ordre

On choisit deux quadruplets de nombres. Pour le premier quadruplet, on prend par exemple a = 1, b = 2, c = 3 et d = 4. On remplace chaque expression du début par sa valeur numérique. Le premier membre est formé de -2 et 11, le second membre par 10 et 5. On choisit 12 comme opérateur. On peut écrire :

14 + 10 + 1 + 23 = 2 + 22 + 7 + 17 = 96

Pour le second quadruplet, on prend par exemple a = 1, b = 2, c = 5 et d = 6. Le premier membre est formé par -4 et 17, le second membre par 16 et 7. On choisit 20 comme opérateur. On peut écrire :

24 + 16 + 3 + 37 = 4 + 36 + 13 + 27 = 80

On peut produire une égalité en additionnant les termes membre par membre. En voici une avec les nombres triangulaires :

1^Δ + 3^Δ + 10^Δ + 14^Δ + 16^Δ + 23^Δ + 24^Δ + 37^Δ = 2^Δ + 4^Δ + 7^Δ + 13^Δ + 17^Δ + 22^Δ + 27^Δ + 36^Δ = 1582

Cette égalité vaut pour les polygonaux de tout ordre. Cela est aussi vrai pour les cubes.

1³ + 3³ + 10³ + 14³ + 16³ + 23³ + 24³ + 37³ = 2³ + 4³ + 7³ + 13³ + 17³ + 22³ + 27³ + 36³ = 84 512

8. Fraction d’une somme

On choisit quatre nombres dont la somme est paire. On divise la somme par 2 et, du quotient, on soustrait chacun des nombres.

Égalité de huit polygonaux du même ordre

Par exemple, on choisit 1, 4, 6 et 7. La somme est 18 et la demi-somme 9.

En soustrayant de 9, on obtient 8, 5, 3, 2. On écrit les nombres choisis dans le premier membre de l’égalité et les autres dans le second membre.

En considérant les nombres hexagonaux, on peut écrire :

1^h + 4^h + 6^h + 7^h = 2^h + 3^h + 5^h + 8^h = 186

Cette égalité qui comprend les entiers de 1 à 8 est vraie pour les polygonaux de tout ordre.

Égalité de 12 polygonaux du même ordre

Pour trouver une égalité comprenant 12 polygonaux, on choisit six éléments au lieu de quatre et on prend le tiers de la somme au lieu de la moitié. Pour le reste, on procède de la même façon.

Choisissons 4, 5, 7, 8, 11, 16. La somme est 51. Le tiers de la somme est 17. De 17, on soustrait chacun de ces six éléments. On obtient : 13, 12, 10, 9, 6, 1.

En considérant les nombres triangulaires, on peut écrire :

4^Δ + 5^Δ + 7^Δ + 8^Δ + 11^Δ + 16^Δ = 1^Δ + 6^Δ + 9^Δ + 10^Δ + 12^Δ + 13^Δ = 291

Cette égalité vaut pour les polygonaux de tout ordre.

Égalité de 16 polygonaux du même ordre

Pour trouver une égalité comprenant 16 polygonaux, on choisit huit éléments et on prend le quart de leur somme. Pour le reste, on procède de la même façon que précédemment.

Choisissons 1, 4, 5, 8, 10, 11, 14, 15. La somme est 68. Le quart de la somme est 17. De 17, on soustrait chacun de ces éléments. On obtient : 16, 13, 12, 9, 7, 6, 3, 2.

En considérant les pentagonaux, on peut écrire :

1^p + 4^p + 5^p + 8^p + 10^p + 11^p + 14^p + 15^p = 2^p + 3^p + 6^p + 7^p + 9^p + 12^p + 13^p + 16^p = 1088

Cette égalité qui contient les entiers de 1 à 16 est vraie pour les polygonaux de tout ordre.

9. Opérations de transformation

Voici quelques propositions qui s’appliquent lorsqu’une égalité est vraie pour les nombres polygonaux de tous les ordres :

• On peut additionner un même nombre à chaque base. On retrouve alors une nouvelle égalité.

Soit l’égalité 1^P + 7^P + 10^P = 2^P + 5^P + 11^P = 216. Par exemple, on additionne 9. On obtient :

10^P + 16^P + 19^P = 11^P + 14^P + 20^P = 1053

• On peut, de chaque base, soustraire un même nombre. On retrouve alors une nouvelle égalité.

Il est fort probable alors que des bases négatives apparaîtront. Pour donner un exemple avec les triangulaires, il faut savoir que 0^Δ = 0, -1^Δ = 0, -2^Δ = 1, -3^Δ = 3, -4^Δ = 6.

• On peut multiplier un même nombre à chaque base. On retrouve alors une nouvelle égalité.

• On peut diviser chaque base par un même nombre. On retrouve alors une nouvelle égalité.

Les bases de ces nouvelles égalités seront composées en grande partie par des nombres fractionnaires. Cela ne rend pas fausse l’égalité, mais elle manque d’élégance.

• On peut ajouter un même chiffre devant chaque base. On retrouve alors une nouvelle égalité.

Dans ce cas, il faut considérer que toutes les bases ont le même nombre de chiffres, quitte à ajouter un ou des 0 devant certains nombres. Par exemple, dans l’égalité 4² + 8² + 11² + 15² = 5² + 6² + 13² + 14², on considère 4, 8, 5 et 6 comme étant 04, 08, 05 et 06. Si on ajoute 1 au début, on peut écrire :

104² + 108² + 111² + 115² = 105² + 106² + 113² + 114² = 48 026

• On peut ajouter un même chiffre après chaque base. On retrouve alors une nouvelle égalité.

À partir de la première égalité du cas précédent, si on ajoute 1 à la fin de chaque base, on peut écrire :

41² + 81² + 111² + 151² = 51² + 61² + 131² + 141² = 43 364

Conclusion

Il est possible de découvrir une très grande quantité d’égalités qui conviennent à tous les ordres de nombres polygonaux : triangulaires, carrés, pentagonaux, hexagonaux, heptagonaux, octogonaux, etc. Ces nombres sont tous du deuxième degré et ont des relations entre eux.

Il est bon de rappeler que les carrés font partie des nombres polygonaux. En conséquence, lorsqu’une identité est vraie pour tout nombre polygonal, elle l’est aussi pour les carrés.